
Seleccione uno
o más idiomas
0,1,3
- Alemán
- Inglés
- Chino
- Español
Frecuencia angular
La frecuencia angular $\omega $ es el cambio en el ángulo de rotación $\Delta \varphi $ por unidad de tiempo $\Delta t$ en un sistema rotativo u oscilante. Es proporcional a la frecuencia f y tiene la siguiente relación con esta: $\omega =2\pi \cdot f $
El símbolo $\nu $ se usa a menudo para la frecuencia, en lugar de $f$ en las fórmulas de ingeniería.
La frecuencia angular puede usarse para definir diferentes relaciones en los campos de la matemática, la mecánica y la ingeniería eléctrica.
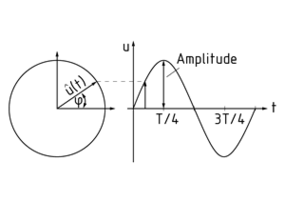
La oscilación armónica puede ser ilustrada por un diagrama de vector. El vector de diagrama tiene una longitud de 1 y se mueve con la frecuencia angular $\omega $. Su proyección hacia un diagrama posición-tiempo ilustra la desviación u para el tiempo relevante t.
La amplitud indica la desviación máxima de la vibración $\hat{u}(t)$ .
Diagrama de vector para una oscilación
Kreisfrequenz
Die Kreisfrequenz $\omega $ beschreibt die Änderung des Drehwinkels $\Delta \varphi $ pro Zeiteinheit $\Delta t$ eines sich drehenden oder schwingenden Systems. Sie ist proportional zu der Frequenz f und hängt wie folgt mit dieser zusammen: \[\omega =2\pi \cdot f\]
In der Technik wird für die Frequenz auch häufig das Formelzeichen $\nu $ statt $f$ verwendet.
Die Kreisfrequenz ist zur Beschreibung diverser mathematischer, mechanischer und elektrotechnischer Zusammenhänge geeignet.
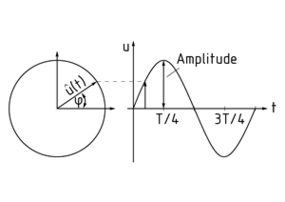
Eine harmonische Schwingung ist durch ein Zeigerdiagramm beschreibbar. Der Zeiger des Diagramms hat die Länge 1 und bewegt sich mit der Kreisfrequenz $\omega $ . Die Projektion des Zeigers auf ein Ort-Zeit-Diagramm veranschaulicht die Größe der Auslenkung u zur jeweiligen Zeit t.
Die Amplitude bezeichnet die maximale Auslenkung der Schwingung $\hat{u}(t)$.
Angular frequency
Angular frequency $\omega $ is the change in the angle of Rotation $\Delta \varphi $ per unit of time $\Delta t$ in a rotating or oscillating system. It is proportional to the frequency f and has the following relationship with it: \[\omega =2\pi \cdot f\]
The symbol $\nu $ is often used for frequency instead of $f$ in engineering formulas.
Angular frequency can be used to define various relationships in the fields of mathematics, Mechanics and electrical engineering.
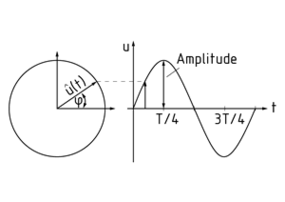
Harmonic Oscillation can be illustrated by a Vector diagram. The diagram vector has a length of 1 and moves with the angular frequency $\omega $. Its projection onto a position-time diagram illustrates the deflection u for the relevant time t.
The amplitude indicates the maximum deflection of the vibration $\hat{u}(t)$.
角频率
角频率 $\omega $ 指在旋转或振荡系统中单位时间 $\Delta t$ 内旋转角度的变化 $\Delta \varphi $ 。 其与 频率f 成正比,遵从如下关系: $\omega =2\pi \cdot f$
在工程公式中,通常使用符号 $\nu $ 来表示频率,而不是 $f$ 。
在数学、力学和电子工程领域,角频率可以用来定义很多不同的关系式。
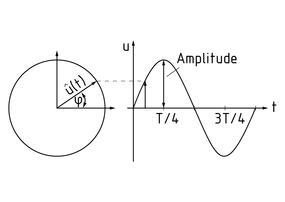
谐振荡可以用矢量图来表示。矢量图长度为 1 并随角频率 $\omega $ 运动。其在位置-时间图上的投影表示在相关时间 t内的挠曲 u。
振幅表示振动的最大挠曲 $\hat{u}(t)$ 。
振动矢量图
