Vector

Vektor im kartesischen Koordinatensystem

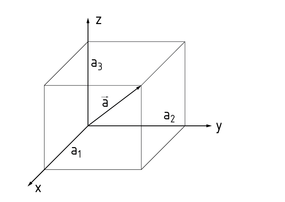
Un vector $\vec{a}$ puede ser visualizado como un segmento de línea dirigido con una longitud específica y una orientación en el espacio n-dimensional. Se representa en forma de matriz con elementos acomodados en una fila $\vec{a}=({{a}_{1}},{{a}_{2}},{{a}_{3}})$ o una columna $\vec{a}=\left( \begin{matrix} {{a}_{1}} \\ {{a}_{2}} \\ {{a}_{3}} \\\end{matrix} \right)$ . El vector es referido como vector de fila o columna (matriz). Los vectores en el espacio tridimensional se llaman vectores espaciales (ver figura). Si un valor ${{a}_{i}}$ es igual a 0, el vector es un vector plano en el espacio bidimensional.

Cada punto en el espacio puede ser descrito por su vector de ubicación (vector de radio, vector de posición), el cual lo conecta con su origen en el sistema de coordenadas. En términos generales, un vector que conecta dos puntos es referido como vector de conexión.

La longitud de un vector corresponde a su magnitud, es decir $\left| {\vec{a}} \right|=\sqrt{{{a}_{x}}^{2}+{{a}_{y}}^{2}+{{a}_{z}}^{2}}$ . Dos vectores de la misma longitud, orientación y dirección son idénticos. Los vectores paralelos comparten la misma orientación y dirección, mientras que los vectores antiparalelos tienen la misma dirección pero orientación opuesta.

El producto vectorial o producto cartesiano se usa para definir vectores perpendiculares. Dos vectores $\vec{a}$ y $\vec{b}$ abarcan un plano. El producto vectorial $\vec{a}\times \vec{b}$ produce un vector perpendicular en el plano abarcado.

Vector en el sistema de coordenadas cartesianas

Vektor

Vektor im kartesischen Koordinatensystem

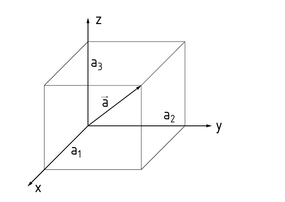
Ein Vektor $\vec{a}$ lässt sich als eine gerichtete Strecke mit einer bestimmten Länge und einer Ausrichtung im n-dimensionalen Raum veranschaulichen. Dargestellt ist ein Vektor in Form einer Matrix mit einer Anordnung von Elementen in einer Zeile $\vec{a}=({{a}_{1}},{{a}_{2}},{{a}_{3}})$ oder einer Spalte \[\vec{a}=\left( \begin{matrix}{{a}_{1}} \\{{a}_{2}} \\{{a}_{3}} \\\end{matrix} \right)\]. Der Vektor wird als Zeilen- oder Spaltenvektor bezeichnet. Vektoren im dreidimensionalen Raum heißen räumliche Vektoren (siehe Bild). Ist ein Wert ${{a}_{i}}$ gleich 0, so handelt es sich um einen ebenen Vektor im zweidimensionalen Raum.

Jeder Punkt in einem Raum ist durch seinen Ortsvektor (Radiusvektor, Positionsvektor), der den Ursprung des Koordinatensystems mit dem Punkt verbindet, beschreibbar. Allgemein wird ein Vektor, der zwei Punkte verbindet, als Verbindungsvektor bezeichnet.

Die Länge eines Vektors entspricht seinem Betrag, für den gilt: $\left| {\vec{a}} \right|=\sqrt{{{a}_{x}}^{2}+{{a}_{y}}^{2}+{{a}_{z}}^{2}}$. Haben zwei Vektoren die gleiche Länge, Orientierung und Richtung, so sind sie gleich. Sind sie in ihrer Orientierung und Richtung gleich, verlaufen sie parallel. Anti-parallel verlaufen Vektoren, die nur die gleiche Richtung haben, aber gegensätzlich orientiert sind.

Senkrecht aufeinander stehende Vektoren lassen sich mithilfe des Vektor- oder auch Kreuzproduktes ermitteln. Zwei Vektoren $\vec{a}$ und $\vec{b}$spannen eine Ebene auf. Das Vektorprodukt $\vec{a}\times \vec{b}$ liefert einen Vektor, der zu der aufgespannten Ebene senkrecht steht.

Vector

Vector in the Cartesian coordinate system

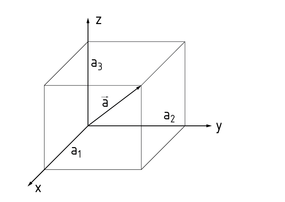
A vector $\vec{a}$ can be visualised as a directed line segment with a specific length and an orientation in n-dimensional space. It is depicted in the form of a Matrix with elements arranged in a row $\vec{a}=({{a}_{1}},{{a}_{2}},{{a}_{3}})$ or a column \[\vec{a}=\left( \begin{matrix}{{a}_{1}} \\{{a}_{2}} \\{{a}_{3}} \\\end{matrix} \right)\]. The vector is referred to as a row or column vector (matrix). Vectors in three-dimensional space are called spatial vectors (see figure). If a value ${{a}_{i}}$ equals 0, the vector is a plane vector in two-dimensional space.

Every point in space can be described by its location vector (radius vector, position vector), which connects it to the origin of the coordinate system. Generally speaking, a vector that connects two points is referred to as a connecting vector.

The length of a vector corresponds to its magnitude, i.e. $\left| {\vec{a}} \right|=\sqrt{{{a}_{x}}^{2}+{{a}_{y}}^{2}+{{a}_{z}}^{2}}$. Two vectors of the same length, orientation and direction are identical. Parallel vectors share the same orientation and direction, while anti-parallel vectors have the same direction but opposite orientations.

The vector product or cross product is used to define perpendicular vectors. Two vectors $\vec{a}$ and $\vec{b}$span a plane. The vector product $\vec{a}\times \vec{b}$ produces a vector perpendicular to the spanned plane.

向量

直角坐标系中的向量

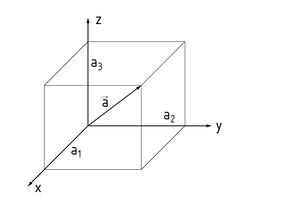
n维空间中的向量 $\vec{a}$ 可以形象化地表示为一个具有特定长度和方向的有向线段。向量可以用矩阵表示，矩阵中的元素可以排列成一行 $\vec{a}=({{a}_{1}},{{a}_{2}},{{a}_{3}})$ 或者排列成一列 $vec{a}=\left( \begin{matrix} {{a}_{1}} \\{{a}_{2}} \\{{a}_{3}} \\\end{matrix} \right)$。这样的向量称为行向量或列向量（亦称行矩阵或列矩阵）。三维空间中的向量也称为空间向量（如图所示）。 如果某个分量 ${{a}_{i}}$ 等于 0，则该向量即为二维空间中的平面向量。

空间中的每一点都可以用它的 位置向量 （矢径，方位向量）来描述，它与坐标原点相连。一般来说，连接两点的向量称为连接向量。

向量的长度就是向量的模，即 $\left| {\vec{a}} \right|=\sqrt{{{a}_{x}}^{2}+{{a}_{y}}^{2}+{{a}_{z}}^{2}}$。两个具有相等长度且相同方向的向量即为相等向量。同向平行 向量具有相同的方向， 而 反向平行 向量则具有相反的方向。

向量积 或 叉乘用来计算法向量。两个向量 $\vec{a}$ a和 $\vec{b}$ 可以确定一个平面。 向量积 $\vec{a}\times \vec{b}$ 就是垂直于该平面的法向量。

直角坐标系中的向量

近义词

半径向量

位置向量

列向量

行向量

连接向量

向量积

叉乘