Teorema de los ejes paralelos

Flächenträgheitsmoment für zusammengesetzte Querschnitte

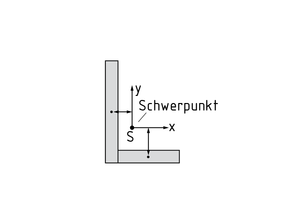
El teorema de los ejes paralelos (teorema de Steiner) se usa para transformar momentos de inercia de área en un eje que va paralelo al eje del centroide (gravedad). En el caso de los componentes que comprenden áreas de sección compuestas, se puede usar el teorema de los ejes paralelos para determinar los momentos de área de secciones completas.

El momento de inercia de área de una sección compuesta (ver diagrama con ejemplo de sección L) se calcula de la siguiente manera:

Dividir la sección completa en formas simples de la sección (por ejemplo, cuadros, triángulos, círculos)

Determinar los centros de gravedad individuales

Calcular los momentos de inercia de área (de las secciones relevantes) u obtener estos valores de las tablas apropiadas ( ${{I}_{y~}}$y ${{I}_{z~}}$ )

Transformar los momentos de inercia de área relevantes mediante el teorema de ejes paralelos: ${{I}_{{\bar{y}}}}={{I}_{y}}+\bar{z}_{s}^{2}A$ , ${{I}_{{\bar{z}}}}={{I}_{z}}+\bar{y}_{s}^{2}A$ , ${{I}_{\bar{y}\bar{z}}}={{I}_{yz}}-\bar{y}_{s}^{{}}\bar{z}_{s}^{{}}A$

$\bar{z}_{s}^{2}A$ y $\bar{y}_{s}^{2}A$ se llaman ambos la proporción de Steiner. El área A relevante es multiplicada por el cuadrado de la distancia entre los centros de gravedad individuales y los comunes.

Sumar los momentos de inercia de área transformados relevantes para obtener un momento de inercia de área total indica el momento de área de la sección completa

Momento de inercia de área para secciones compuestas

Steinerscher Satz

Flächenträgheitsmoment für zusammengesetzte Querschnitte

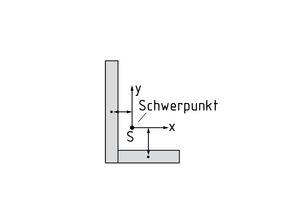
Der Steinersche Satz dient zur Transformation der Flächenträgheitsmomente auf eine Achse, die parallel zur Schwerachse verläuft. Bei Bauteilen aus zusammengesetzten Querschnittsflächen kann mit dem Steinersche Satz die Flächenmomenten der Gesamtquerschnitte bestimmt werden.

Das Flächenträgheitsmoment eines zusammengesetzten Querschnittes (s. Abbildung: Beispiel eines L-Profils) wird folgendermaßen berechnet:

• Aufteilung des Gesamtquerschnitts in einfache Querschnittsformen (z. B. Quadrat, Dreieck, Kreis)
• Ermittlung der Einzelschwerpunkte
• Berechnung der Flächenträgheitsmomente (der jeweiligen Querschnitte) oder Ablesen dieser Werte aus geeigneten Tabellen (${{I}_{y~}}$und ${{I}_{z~}}$)
• Transformation der jeweiligen Flächenträgheitsmomente durch die Verwendung des Steinerschen Satzes: \[{{I}_{{\bar{y}}}}={{I}_{y}}+\bar{z}_{s}^{2}A\], ${{I}_{{\bar{z}}}}={{I}_{z}}+\bar{y}_{s}^{2}A$, \[{{I}_{\bar{y}\bar{z}}}={{I}_{yz}}-\bar{y}_{s}^{{}}\bar{z}_{s}^{{}}A\]

Dabei wird jeweils $\bar{z}_{s}^{2}A$ und \[\bar{y}_{s}^{2}A\] als Steinerscher Anteil bezeichnet. In diesem wird die jeweilige Fläche A mit dem Quadrat des Abstandes von Einzelschwerpunkt zum Gesamtschwerpunkt multipliziert.

• Die Addition der jeweiligen transformierten Flächenträgheitsmomente zu einem gesamten Flächenträgheitsmoment ergibt das Flächenmoment des Gesamtquerschnittes

Parallel-axis theorem

Area moment of inertia for composite cross-sections

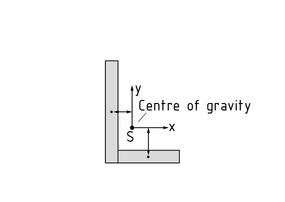
The parallel-axis theorem (Steiner's theorem) is used to transform area moments of inertia onto an axis running parallel to the centroid (gravity) axis. In the case of components comprising composite cross-sectional areas, the parallel-axis theorem can be used to determine the area moments of the full cross-sections.

The Area moment of inertia of a composite cross-section (see diagram with example of L section) is calculated as follows:

• Split the full cross-section into simple cross-sectional shapes (e.g. square, triangle, circle)
• Determine the individual centres of gravity
• Calculate the area moments of inertia (of the relevant cross-sections) or obtain these values from appropriate tables (${{I}_{y~}}$and ${{I}_{z~}}$)
• Transform the relevant area moments of inertia using the parallel-axis theorem: \[{{I}_{{\bar{y}}}}={{I}_{y}}+\bar{z}_{s}^{2}A\], ${{I}_{{\bar{z}}}}={{I}_{z}}+\bar{y}_{s}^{2}A$, \[{{I}_{\bar{y}\bar{z}}}={{I}_{yz}}-\bar{y}_{s}^{{}}\bar{z}_{s}^{{}}A\]

$\bar{z}_{s}^{2}A$ and \[\bar{y}_{s}^{2}A\] are both called the Steiner's share. The relevant area A is multiplied by the square of the distance between the individual and common centres of gravity.

• Adding up the relevant transformed area moments of inertia to obtain a total area moment of inertia indicates the area moment of the full cross-section

平行轴定理

多种横截面的面积惯性矩

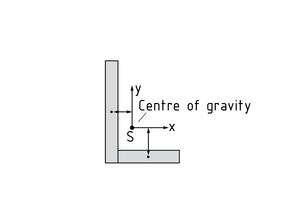
平行轴定理 （史丹纳定理）可以从质心（重心）的面积惯性矩，计算出任一平行于质心的轴上的面积惯性矩。对于包含有多种横截面的构件，平行轴定理可用于确定所有截面上惯性矩的合矩。

包含有多种横截面的构件（见图中的 L 型构件）的面积惯性矩计算如下：

将全部横截面拆分为简单的横截面形状（如正方形，三角形，圆形）

确定各自的重心

计算各自（相关截面)的面积惯性矩或从合适的表 ( ${{I}_{y~}}$ 和 ${{I}_{z~}}$ )中选取数值

使用平行轴定理进行面积惯性矩的转换计算： ${{I}_{{\bar{y}}}}={{I}_{y}}+\bar{z}_{s}^{2}A$, ${{I}_{{\bar{z}}}}={{I}_{z}}+\bar{y}_{s}^{2}A$, ${{I}_{\bar{y}\bar{z}}}={{I}_{yz}}-\bar{y}_{s}^{{}}\bar{z}_{s}^{{}}A$

$\bar{z}_{s}^{2}A$ 和 $\bar{y}_{s}^{2}A$ 都被称为史丹纳面。面积元素 A 乘以各自重心和公共重心间距离的平方。

将各个截面的面积惯性矩进行积分求和运算，得到所有截面的总体面积惯性矩。

多种横截面的面积惯性矩