Movimiento plano en coordinadas polares

Radialkoordinate und Winkelkoordinate

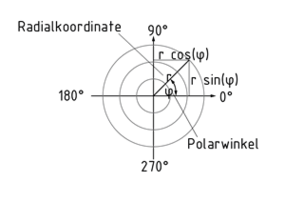
El término coordenadas polares se refiere a un sistema coordinado bidimensional en el cual la posición de cualquier punto puede definirse basada en un ángulo $\varphi $ y la distancia r desde el origen del sistema coordinado.

La distancia r es referida como la coordinada radial. La coordenada angular $\varphi $ (también ángulo polar) proporciona información sobre el número de grados en que un punto es removido desde el eje polar en una dirección matemáticamente positiva (en el sentido contrario a las manecillas del reloj).

Los movimientos expresados en coordenadas polares son establecidos en sus componentes de velocidad. Este desglose en componentes por separado se lleva a cabo en una dirección radial y otra perpendicular. El vector de velocidad $\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ comprende los siguientes componentes: $\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }} $ donde ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ y ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$

Coordenadas radiales y coordenadas angulares

Ebene Bewegung in Polarkoordinaten

Radialkoordinate und Winkelkoordinate

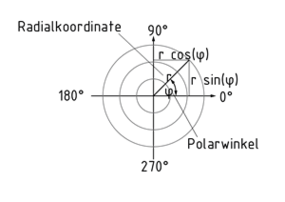
Als Polarkoordinaten wird ein zweidimensionales Koordinatensystem bezeichnet, in dem die Position eines Punktes durch einen Winkel $\varphi $ und den Abstand r vom Ursprung des Koordinatensystems angegeben wird.

Der Abstand r nennt sich Radialkoordinate. Die Winkelkoordinate $\varphi $ (auch Polarwinkel) gibt darüber Auskunft, um wieviel Grad ein Punkt in mathematisch positiver Richtung (linksdrehend) von der Polarachse entfernt ist.

In Polarkoordinaten ausgedrückte Bewegungen werden durch ihre Geschwindigkeitskomponenten angegeben. Diese Zerlegung in Komponenten wird in radialer und dazu senkrechter Richtung durchgeführt. Der Geschwindigkeitsvektor$\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ setzt sich wie folgt zusammen: \[\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }}\] mit ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ und ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$

Planar motion in polar coordinates

Radial coordinates and angular coordinates

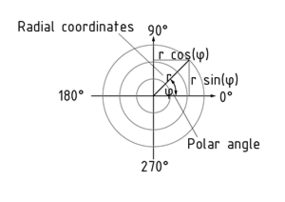
The term polar coordinates refers to a two-dimensional coordinate system in which the position of any one point can be defined based on an angle $\varphi $ and the distance r from the origin of the coordinate system.

The distance r is referred to as the radial coordinate. The angular coordinate $\varphi $ (also polar angle) provides information on the number of degrees that a point is removed from the polar axis in a mathematically positive direction (counter-clockwise).

Movements expressed in polar coordinates are stated in their Velocity components. This breakdown into separate components is carried out in a radial and perpendicular direction. The velocity vector $\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ comprises the following components: \[\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }}\] where ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ and ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$

极坐标中的平面运动

径向坐标和角坐标

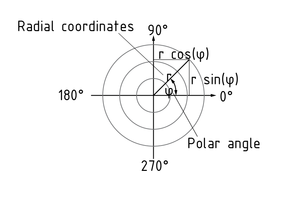
极坐标系是一个二维坐标系，在该坐标系中任意一点都可以用角度 $\varphi $ 和与坐标系原点间的距离r来表示

径向坐标指距离r。角坐标（也称为极角） $\varphi $ 为一点以数学正方向（逆时针）绕极轴旋转的角度。

极坐标中物体的运动可由其速度分量表示。速度可在径向和法向进行分解。速度矢量 $\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ 包括以下分量：$\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }}$ 在 ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ 和 ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$

径向坐标和角坐标