
Seleccione uno
o más idiomas
0,1,3
- Alemán
- Inglés
- Chino
- Español
Análisis de Fourier
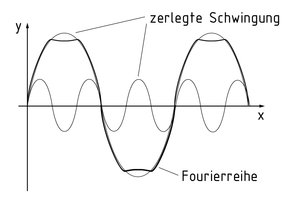
El análisis de Fourier es el estudio de las integrales y series de Fourier. Una serie de Fourier es una expansión de serie de una función en una serie de funciones de seno y coseno. Esta es seccionalmente continua y periódica.
El análisis de Fourier descompone una serie de Fourier en las oscilaciones mostradas por las funciones trigonométricas básicas. La figura muestra una gráfica representada por un análisis de Fourier con dos oscilaciones.
Una serie de Fourier se estructura de la siguiente manera:
$f(x)=\frac{{{a}_{0}}}{2}+\sum\limits_{n=1}^{\infty }{[{{a}_{n}}\cos (nx)+{{b}_{n}}\sin (nx)]}$ .
El intervalo de la función cae entre $-\pi $ y $\pi $ . Se deben determinar los coeficientes ${{a}_{0}}$ , ${{a}_{n}}$ y ${{b}_{n}}$ . ${{a}_{n}}$ y ${{b}_{n}}$ son coeficientes de Fourier.
Descomposición mediante el análisis de Fourier
Fourier-Analyse
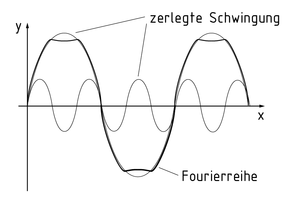
Die Fourier-Analyse beschäftigt sich mit den Fourierreihen und -integralen. Eine Fourierreihe ist eine Reihenentwicklung einer Funktion in einer Funktionsreihe aus Kosinus- und Sinus-Funktionen. Sie ist abschnittsweise stetig und verläuft periodisch.
Wird eine Fourierreihe in die durch die trigonometrischen Basisfunktionen dargestellten Schwingungen zerlegt, so wird von Fourier-Analyse gesprochen. Im Bild ist ein Graph dargestellt, der durch eine Fourier-Analyse mit zwei Schwingungen dargestellt wird.
Aufgebaut ist eine Fourierreihe wie folgt:
Das Intervall der Funktion liegt zwischen $-\pi $ und $\pi $. Die Koeffizienten${{a}_{0}}$, ${{a}_{n}}$ und ${{b}_{n}}$ sind zu bestimmen. ${{a}_{n}}$ und ${{b}_{n}}$sind die sog. Fourierkoeffizienten.
Fourier analysis
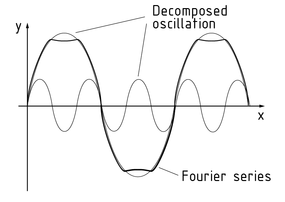
Fourier analysis is the study of Fourier series and integrals. A Fourier series is a series expansion of a function in a series of cosine and sine functions. It is sectionally continuous and periodic.
Fourier analysis decomposes a Fourier series into the oscillations depicted by the basic trigonometrical functions. The figure shows a graph depicted by a Fourier analysis with two oscillations.
A Fourier series is structured as follows:
The interval of the function lies between $-\pi $ and $\pi $. The coefficients ${{a}_{0}}$, ${{a}_{n}}$ and ${{b}_{n}}$ need to be determined. ${{a}_{n}}$ and ${{b}_{n}}$are Fourier coefficients.
傅里叶分析
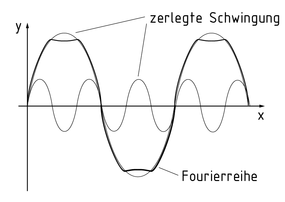
傅里叶分析主要研究傅里叶级数和傅里叶积分。傅里叶级数可将一个函数展开成余弦与正弦函数的级数形式。它是分段连续的,且是周期函数。
傅里叶分析将傅里叶级数分解成由三角函数表达的震荡。右图呈现了带有两组震荡的傅里叶分析图像。
傅里叶级数有如下结构:
$f(x)=\frac{{{a}_{0}}}{2}+\sum\limits_{n=1}^{\infty }{[{{a}_{n}}\cos (nx)+{{b}_{n}}\sin (nx)]}$
函数的定义区间介于 $-\pi $ 和 $\pi $。系数 ${{a}_{0}}$, ${{a}_{n}}$ 和 ${{b}_{n}}$ 需要确定。 ${{a}_{n}}$ 和 ${{b}_{n}}$ 叫做傅里叶系数。
利用傅里叶分析进行分解
近义词
经典调和分析
傅里叶级数
傅里叶系数
