Casos de pandeo de Euler

Eulersche Knickfälle

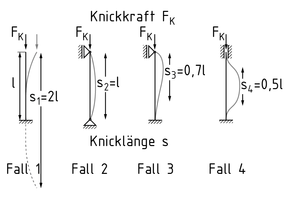
Los casos de pandeo de Euler definen las posibles formas de pandeo en los cuerpos delgados (vigas, miembros, etc.). El pandeo ocurre como resultado de una fuerza de compresión longitudinal que causa que el cuerpo o el miembro pierda su estabilidad. En el caso del pandeo, el miembro se deforma. La falla puede producirse repentinamente.

La fuerza con la que el proceso de pandeo comienza se llama fuerza de pandeo ${{K}_{B}}$ . Para todo pandeo en el rango elástico, esta fuerza se calcula de la siguiente manera: ${{F}_{B}}=\frac{{{\pi }^{2}}EI}{{{s}^{2}}}$ (módulo de elasticidad E; momento de inercia de área axial I; longitud de pandeo s).

La longitud de pandeo s y, por lo tanto, la línea de pandeo dependen de cómo se sujeta el miembro. En soportes fijos (trivalentes), el miembro siempre es tangencialmente adyacente.

Para los cuatro casos de Euler, la longitud de pandeo s depende de la longitud del miembro L y de un coeficiente de longitud de pandeo $\beta $ .

Caso 1: fijo/libre - $\beta =2 $ : ${{s}_{1}}=2\cdot L $

Caso 2: articulado/articulado - $\beta =1 $ : ${{s}_{2}}=1\cdot L $

Caso 3: fijo/articulado - $\beta =0.699 $ : ${{s}_{3}}=0.699\cdot L $

Caso 4: fijo/fijo - $\beta =0.5 $ : ${{s}_{4}}=0.5\cdot L $

Pandeo de Euler

Eulersche Knickfälle

Eulersche Knickfälle

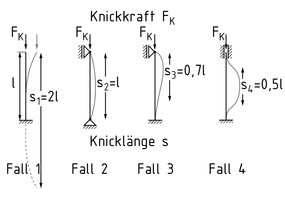
Die Eulerschen Knickfälle beschreiben die möglichen Knickformen von schlanken Körpern (Balken, Stäbe etc.). Das Knicken erfolgt bei einer wirkenden Druckkraft in Längsrichtung, weil der Körper bzw. Stab seine Stabilität verliert. Im Knickfall krümmt sich der Stab. Das Versagen kann schlagartig eintreten.

Die Kraft, ab der der Knickvorgang beginnt, wird als Knickkraft${{F}_{K}}$bezeichnet. Sie berechnet sich für alle Knickfälle im elastischen Bereich mit: ${{F}_{K}}=\frac{{{\pi }^{2}}EI}{{{s}^{2}}}$ (Elastizitätsmodul E

Die Knicklänge s und somit die Knicklinie sind von der Einspannung des Stabes abhängig. In Festlagern (3-wertig) ist der Stab immer tangential anliegend.

Für die vier Eulerfälle ergibt sich die jeweilige Knicklänge s in Abhängigkeit der Stablänge L und einem Knicklängenbeiwert $\beta $.

• Fall 1: eingespannt/frei - $\beta =2$: ${{s}_{1}}=2\cdot L$:
• Fall 2: gelenkig/gelenkig - $\beta =1$: ${{s}_{2}}=1\cdot L$
• Fall 3: eingespannt/gelenkig - $\beta =0,699$: ${{s}_{3}}=0,699\cdot L$
• Fall 4: eingespannt/eingespannt - $\beta =0,5$: ${{s}_{4}}=0,5\cdot L$

Euler buckling cases

Euler buckling

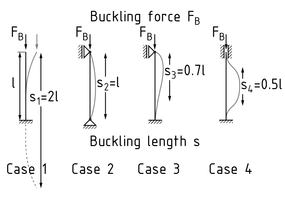
Euler buckling cases define the possible forms of buckling in thin bodies (beams, members, etc.). Buckling occurs as a result of a longitudinal compressive Force that causes the body or member to lose its stability. In the event of buckling, the member warps. Failure can occur suddenly.

The force at which the buckling process starts is called the buckling force${{K}_{B}}$. For all buckling in the elastic range, this force is calculated as follows: ${{F}_{B}}=\frac{{{\pi }^{2}}EI}{{{s}^{2}}}$ (Modulus of elasticity E

The buckling length s and thus the buckling line depend on how the member is attached. In fixed supports (trivalent), the member is always tangentially adjacent.

For the four Euler cases, the relevant buckling length s depends on the member length L and a buckling length coefficient $\beta $.

• Case 1: clamped/free - $\beta =2$: ${{s}_{1}}=2\cdot L$:
• Case 2: articulated/articulated - $\beta =1$: ${{s}_{2}}=1\cdot L$
• Case 3: clamped/articulated - $\beta =0.699$: ${{s}_{3}}=0.699\cdot L$
• Case 4: clamped/clamped - $\beta =0.5$: ${{s}_{4}}=0.5\cdot L$

欧拉屈曲案例

欧拉屈曲

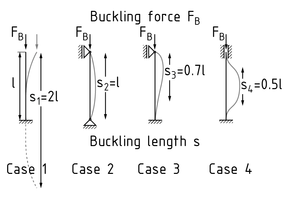
欧拉屈曲案例 定义了细长物体（如梁、杆件等）屈曲的可能情况。屈曲发生是由于构件纵轴方向受到压力，导致其丧失保持 稳定平衡的能力。在屈曲情况下，杆件弯折，瞬间可能发生失效。

屈曲过程的起始力称为屈曲临界力{{K}_{B}}$。弹性范围内的所有情况下的屈曲，屈曲临界力的计算公式如下： ${{F}_{B}}=\frac{{{\pi }^{2}}EI}{{{s}^{2}}}$ (弹性模量 E；截面二次轴矩 I；屈曲长度 s）。

屈曲长度 s 和屈曲线由杆件上力的接触方式决定。固定支撑（三角形支撑）情况下，杆件屈曲线总是具有一条切线。

下面四种不同欧拉屈曲案例具有不同的屈曲长度 s，这取决于杆件长度 L 和有效屈曲长度因子 $\beta $ 。

案例1： 一端固定一端自由 - $\beta =2$ : ${{s}_{1}}=2\cdot L$ :

案例2： 两端铰支 - $\beta =1$ : ${{s}_{2}}=1\cdot L$

案例3： 一端固定一端铰支 - $\beta =0.699$ : ${{s}_{3}}=0.699\cdot L$

案例4： 两端固定 - $\beta =0.5$ : ${{s}_{4}}=0.5\cdot L$

欧拉屈曲