Círculo de curvatura

Krümmungskreis an einer Bahnkurve

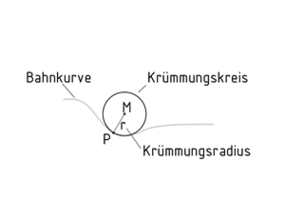
El círculo de curvatura (también círculo osculador) en un punto P de una trayectoria es un círculo que describe o se acerca a la curva en este punto. El círculo de curvatura es definido por tres puntos distintos que se acomodan infinitamente cerca uno de otro. El círculo de curvatura tiene un centro de curvatura M y un radio r, el cual es referido como el radio de curvatura.

Es útil conocer la magnitud del radio de curvatura cuando se determina el componente normal de aceleración en una trayectoria curva, por ejemplo. El tamaño del círculo de curvatura es también importante cuando se determina la distorsión causada por el efecto de un momento de flexión.

Círculo de curvatura de una trayectoria

Krümmungskreis

Krümmungskreis an einer Bahnkurve

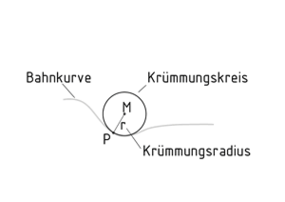
Ein Krümmungskreis (auch Schmiegekreis) einer Bahnkurve im Punkt P ist ein Kreis, welcher die Kurve an dieser Stelle beschreibt bzw. sich ihr annähert. Drei unendlich dicht nebeneinander liegende Punkte auf der Kurve definieren den Krümmungskreis. Der Krümmungskreis hat einen Krümmungsmittelpunkt M und einen Radius r, der als Krümmungsradius bezeichnet wird.

Die Kenntnis der Krümmungsradius-Größe ist zum Beispiel bei der Ermittlung der Normalbeschleunigung auf einer gekrümmten Bahn von Bedeutung. Auch bei der Bestimmung der Verformung durch die Einwirkung eines Biegemoments ist die Größe des Krümmungskreises wichtig.

Circle of curvature

Circle of curvature on a trajectory

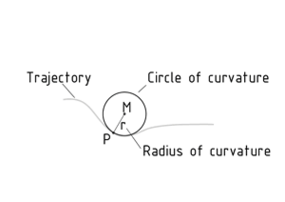
The circle of curvature (also osculating circle) at point P of a trajectory is a circle that describes or comes very close to the curve at this point. The circle of curvature is defined by three distinct points that are arranged infinitely close to each other. The circle of curvature has a centre of curvature M and a radius r, which is referred to as the radius of curvature.

It is useful to know the magnitude of the radius of curvature when determining the Normal component of acceleration on a curved trajectory, for example. The size of the circle of curvature is also important when determining distortion caused by the effect of a Bending moment.

曲率圆

轨迹的曲率圆

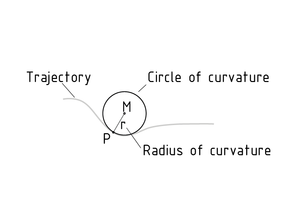
给定曲线上一点P，过P点且与曲线无限接近的圆称为曲线在P点处的曲率圆（又称密切圆）。曲率圆可由三个不同但又无限接近的点来定义。曲率圆中包括曲率中心M和半径r，该半径可称为曲率半径。

例如物体做曲线运动，在计算法向加速度的大小时，需首先确定对应曲率半径的值。曲率圆的大小对确定物体在弯矩作用下的扭曲变形程度也十分重要。

轨迹的曲率圆