Kreisfrequenz
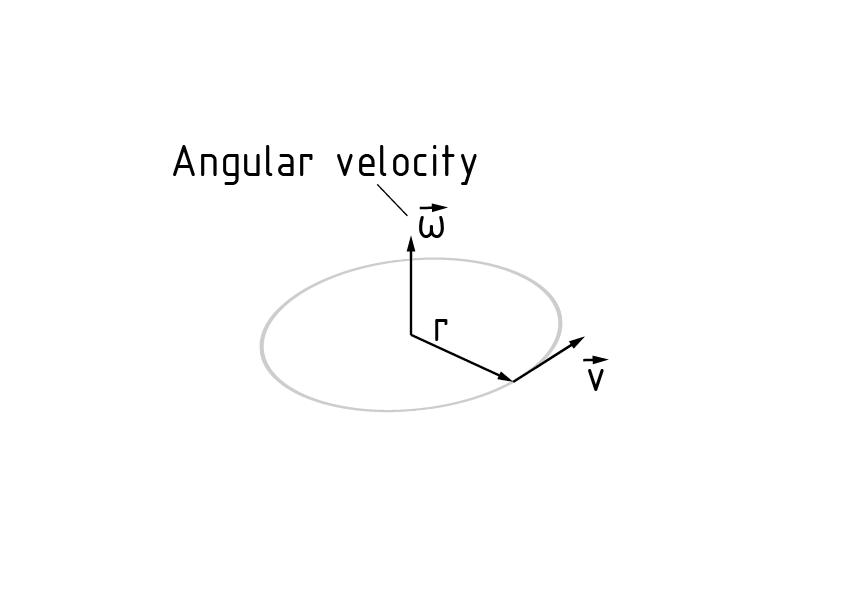
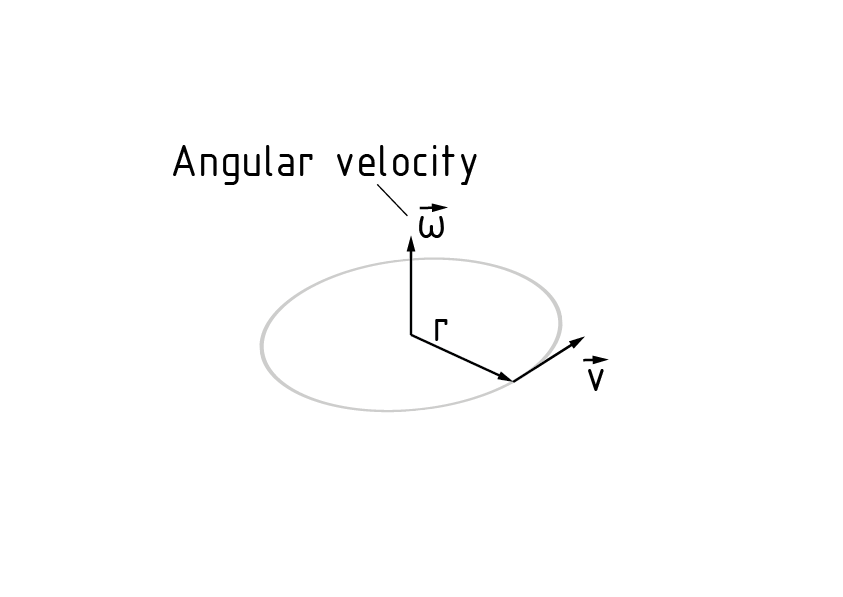
Die Kreisfrequenz $\omega $ beschreibt die Änderung des Drehwinkels $\Delta \varphi $ pro Zeiteinheit $\Delta t$ eines sich drehenden oder schwingenden Systems. Sie ist proportional zu der Frequenz f und hängt wie folgt mit dieser zusammen: \[\omega =2\pi \cdot f\]
In der Technik wird für die Frequenz auch häufig das Formelzeichen $\nu $ statt $f$ verwendet.
Die Kreisfrequenz ist zur Beschreibung diverser mathematischer, mechanischer und elektrotechnischer Zusammenhänge geeignet.
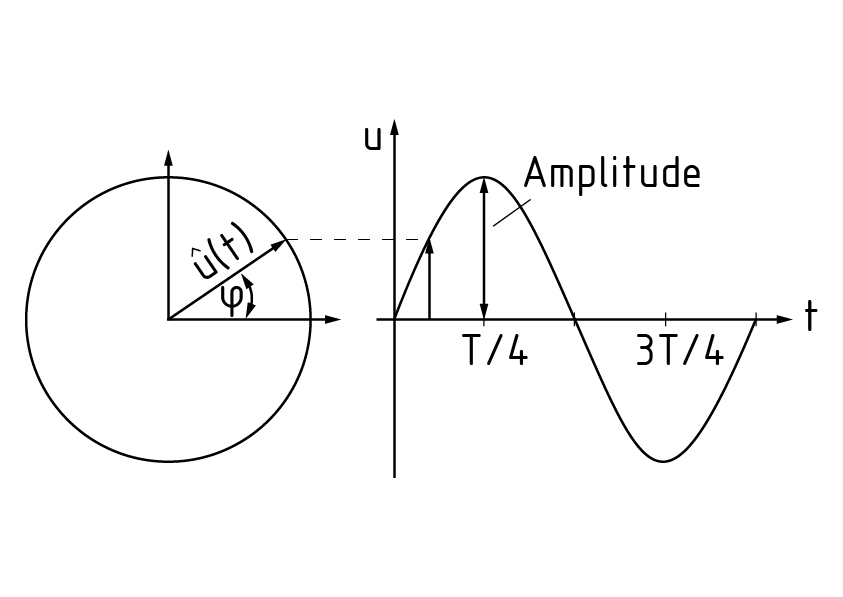
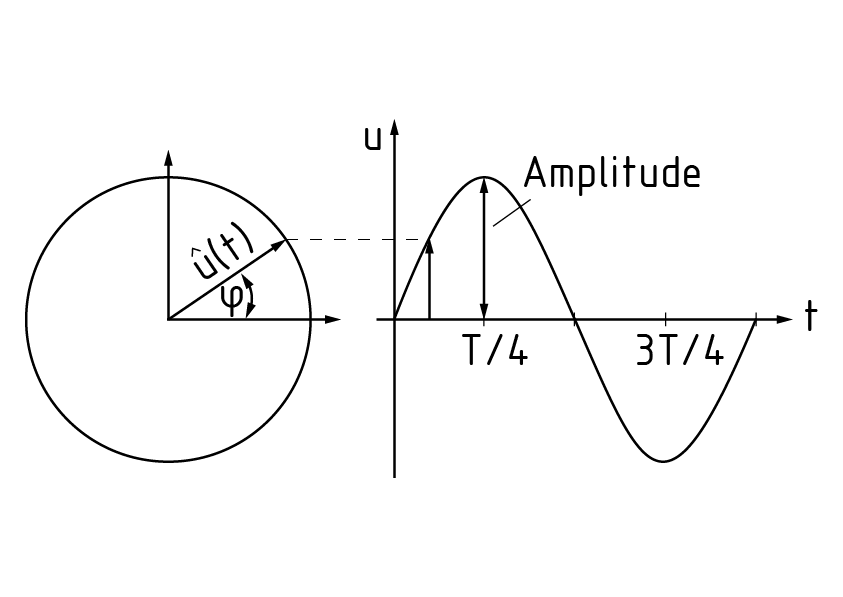
Eine harmonische Schwingung ist durch ein Zeigerdiagramm beschreibbar. Der Zeiger des Diagramms hat die Länge 1 und bewegt sich mit der Kreisfrequenz $\omega $ . Die Projektion des Zeigers auf ein Ort-Zeit-Diagramm veranschaulicht die Größe der Auslenkung u zur jeweiligen Zeit t.
Die Amplitude bezeichnet die maximale Auslenkung der Schwingung $\hat{u}(t)$.
-
Beispielsätze:
- Im Wechselstromkreis ruft eine Induktivität einen induktiven Blindwiderstand hervor, der sich ohne Betrachtung des Phasenverschiebungswinkels aus dem Produkt von der Kreisfrequenz ?
- und der Induktivität ergibt.

angular frequency
-
Example sentences:
- In an AC circuit, an inductance produces an inductive reactance which, ignoring the phase shift angle, is the product of the angular frequency ?

angular speed

circular frequency

radian frequency

frecuencia angular

frecuencia circular

frecuencia en radianes

velocidad angular

圆频率

角速度

角频率