Torsion

Torsion an einem zylindrischen Bauteil

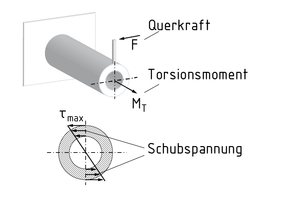
Eine Torsion ist ein Belastungszustand, der durch das Wirken eines Torsionsmomentes M_T eine Verdrehung $\vartheta $ hervorruft. Ein Torsionsmoment entsteht z. B. beim Wirken einer Querkraft und eines Hebelarms d.

Die Verformung ist abhängig von der Querschnittgeometrie des tordierten Bauteils. So tritt beispielsweise an Bauteilen mit rundem Querschnitt keine Verwölbung auf. Abhängig von dem wirkenden Torsionsmoment M_T , dem werkstoffabhängigen Schubmodul G, der Geometrie des Querschnittes und dem daraus resultierenden Torsionsträgheitsmoment I_T ist die Verdrehung pro Längeneinheit $\frac{d\vartheta }{dx}$ berechenbar.

Für Torsionen gilt im Allgemeinen: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$. Das Torsionsträgheitsmoment ${{I}_{T}}$ entspricht bei einem Bauteil mit kreisförmigem Querschnitt dem polaren Flächenträgheitsmoment ${{I}_{P}}$. Im Randbereich dieses Bauteils wirken die größten Schubspannungen $\tau $. Die maximale Schubspannung berechnet sich wie folgt: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{W}_{T}}}$ . Das Torsionswiderstandsmoment W_T repräsentiert die Querschnittgeometrie des Bauteils des Bauteils.

Torsion

Torsion on a cylindrical component

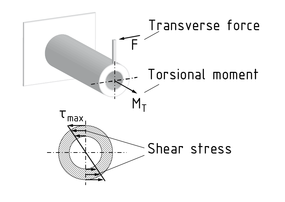
Torsion is a load state that causes twisting $\vartheta $ due to the action of a torsional moment M_T. A torsional moment is created, for example, by the action of a transverse Force and a lever arm d.

The deformation depends on the cross-sectional geometry of the component being twisted. Components with a round cross-section, for example, do not exhibit any warping. The twisting per unit of length $\frac{d\vartheta }{dx}$ can be calculated based on the active torsional moment M_T , the material-dependent shear modulus G, the cross-sectional geometry and the resultant torsional moment of inertia I_T.

The following generally applies to torsions: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$. In the case of a component with a circular cross-section, the torsional moment of inertia ${{I}_{T}}$ is equivalent to the polar Area moment of inertia ${{I}_{P}}$. The largest shear stresses $\tau $ are found at the edges of this component. The maximum Shear stress is calculated as follows: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ . The torsional Resistance moment ${{R}_{T}}$ represents the component's cross-sectional geometry.

扭转

圆形截面体的扭转

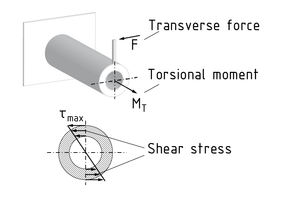
扭转是指以扭矩 MT形式作用于物体上并产生扭曲 $\vartheta $ 的受力与变形形式。扭矩的建立需要很多条件，如横向力和杠杆臂d。

形变量取决于被扭曲构件横截面的几何形状。例如，一个圆形横截面的组件，不产生任何翘曲。单位长度的扭曲 $\frac{d\vartheta }{dx}$ 可以根据以下物理量来计算：主动扭矩 ${{M}_{T}}$ ，材料特性相关的剪切模量 G，横截面的几何形状和扭转惯性矩 ${{I}_{T}}$ 。

下式为扭力计算公式： $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$ 。 构件具有圆形截面时，扭转惯性矩 ${{I}_{T}}$ 等于 截面极惯性矩 ${{I}_{P}}$ 。 最大剪应力 $\tau $ 作用于构件边缘。且剪应力最大值的计算公式如下： ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ 。 扭转阻力矩 ${{R}_{T}}$ 反映了构件的横截面几何形状。

圆形截面体的扭转

Torsión

Torsión en un componente cilíndrico

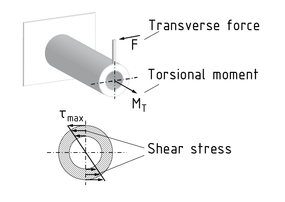
La torsión es un estado de carga que causa un retorcimiento $\vartheta $ debido a la acción de un momento de torsión ${{M}_{T}}$ . Un momento de torsión es creado, por ejemplo, por la acción de una fuerza transversal y un brazo de palanca d.

La deformación depende de la geometría de la sección del componente que se está torciendo. Los componentes con una sección redonda, por ejemplo, no presentan ninguna combadura. La torsión por unidad de longitud $\frac{d\vartheta }{dx}$ puede ser calculada basada en el momento de torsión ${{M}_{T}}$ activo, el módulo de fcorte G dependiente del material, la geometría de la sección y el momento de inercia de torsión ${{I}_{T}}$ resultante.

Lo siguiente aplica generalmente a las torsiones: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$ . En el caso de un componente con una sección circular, el momento de inercia de torsión ${{I}_{T}}$ es equivalente al momento de inercia de área polar ${{I}_{P}}$ . Los esfuerzos de corte más grandes $\tau $ se encuentran en los extremos de este componente. El esfuerzo de corte máximo se calcula de la siguiente manera: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ . El momento de resistencia de torsión ${{R}_{T}}$ representa la geometría de la sección del componente.

Torsión en un componente cilíndrico