Korrelationsdiagramm

Korrelationsdiagramme

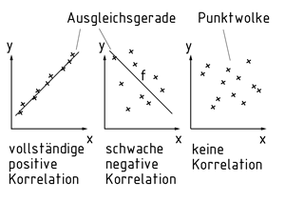
Ein Korrelationsdiagramm wird eingesetzt, um den Zusammenhang zwischen zwei Merkmalen als Wertepaar (x/y) darzustellen. Dazu werden die Merkmale in einem rechtwinkligen Koordinatensystem eingetragen. Aus dem Muster (Punktwolke) des entstehenden Streudiagramms kann erkannt werden, in welcher Abhängigkeit die beiden Merkmale zueinander stehen.

Die Quantifizierung der Stärke des Zusammenhangs zwischen den beiden Merkmale ermittelt die Regressionsanalyse. Mit der Methode der kleinsten Quadrate wird eine Ausgleichsgerade f durch die Punktwolke gelegt. Die Steigung der Gerade bestimmt die Richtung des Zusammenhangs

Korrelieren zwei Merkmale vollständig $(\left| r \right| = 1)$, so liegen alle Messwerte im zweidimensionalen Koordinatensystem auf einer Geraden. Die Gerade steigt bei perfekter positiver Korrelation (r = +1)

Das Korrelationsdiagramm gehört zu den 'Seven Tools' des Qualitätsmanagements.

Scatter diagram

Correlation diagrams

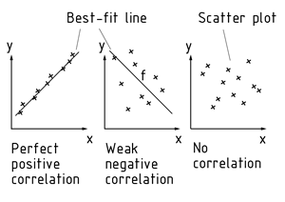
A scatter diagram is used to display the correlation between two variables as a value pair (x/y). To this end, the variables are entered in a Cartesian (rectangular) coordinate system. The pattern (scatter plot) of the resultant scatter diagram shows the dependence between the two variables.

A regression analysis quantifies the Strength of the relationship between the two variables. The method of least squares is used to lay a best-Fit line f through the scatter plot. The slope of the line determines the direction of the correlation

If there is complete correlation between two variables $(\left| r \right| = 1)$, all values in the two-dimensional coordinate system lie on a line. In the case of perfect positive correlation (r = +1), the line slopes up. In the case of perfect negative correlation (r = -1), the line slopes down.

The scatter diagram is one of the "Seven Tools" of Quality management.

散点图

相关图

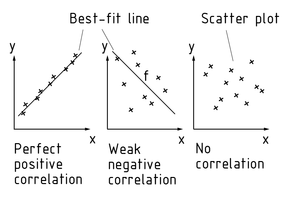
散点图显示作为数值对 （x / y） 的两个变量之间的相关性。为此，变量可表示在笛卡尔（直角）坐标系统中。所得散点图的图案（散点图）显示出了两个变量之间的依存关系。

回归分析量化两个变量之间的关系相关程度。最小平方法用于绘制散点图的最佳拟合线f。直线的斜率确定相关性的方向；无量钢的相关系数值 ${r_{xy}}$ 描述了两个变量之间的相关程度。

如果有两个变量之间完全相关 $(\left| r \right| = 1)$ ，那么平面坐标系统中的所有变量值在一条直线上。在完全正相关 （r = + 1） 的情况下，直线向上倾斜。在完全负相关 （r = -1） 的情况下，直线向下倾斜。

散点图是质量管理的“ ”之一。

相关图

近义词

散点图

Diagrama de dispersión

Diagramas de relación

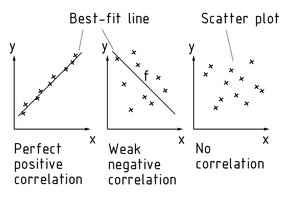
Se usa un diagrama de dispersión para mostrar la relación entre dos variables como un par de valor (x/y). En este sentido, los variables se ingresan en un sistema de coordenadas cartesianas (rectangular). El patrón (trazado disperso) del diagrama disperso resultante muestra la dependencia entre las dos variables.

Un análisis de regresión cuantifica la fuerza de la relación entre dos variables. El método de mínimos cuadrados se usa para colocar una línea de mejor ajuste f a lo largo del trazado disperso. La pendiente de la línea determina la dirección de la relación; el valor del coeficiente de relación sin dimensiones ${r_{xy}}$ describe la fuerza de la relación entre las dos variables.

Si hay una relación completa entre dos variables $(\left| r \right| = 1)$ , todos los valores en el sistema de coordenadas bidimensionales caen en una línea. En el caso de una relación positiva perfecta (r = +1), la línea tiene una pendiente ascendente. En el caso de una relación negativa perfecta (r = -1), la línea tiene una pendiente descendiente.

El diagrama de dispersión es una de las "" de la administración de la calidad.

Diagramas de relación