
Wählen Sie eine
oder mehrere Sprachen aus
0,1,0
- Deutsch
- Englisch
- Chinesisch
- Spanisch
Inertialsystem
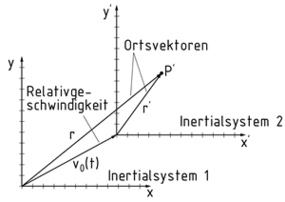
Ein Inertialsystem ist ein Koordinatensystem, in dem Körper ohne Krafteinwirkung eine gleichförmige, geradlinige Bewegung ausführen. Dieses Verhalten basiert auf dem Trägheitsgesetz von Galilei. Trägheit beschreibt das Verhalten eines Körpers, seine Bewegung beizubehalten, solange keine Kraft auf ihn wirkt. Die Größe der Trägheit ist proportional zur Größe der Körpermasse, die auch als Punktmasse betrachtet werden kann.
Ein Punkt P lässt sich durch die Ortsvektoren der jeweiligen Inertialsysteme beschreiben. Im Bild beschreibt $\vec{{r}'}$die Lage des Punktes P. Sie wird durch die Galilei-Transformation bezogen auf ein anderes Inertialsystem wie folgt ermittelt: ${\vec{r}}'=\vec{r}-{{\vec{v}}_{0}}t$. Dabei ist ${{\vec{v}}_{0}}$die Relativgeschwindigkeit und t die Zeit.
Die Beachtung von Inertialsystemen ist bei Bewegungsvorgängen von großer Wichtigkeit. Sie müssen zur eindeutigen Bewertung auf ein Bezugssystem betrachtet werden.
Beispiel: Eine Person bewegt sich in einem langsam fahrenden Zug. Dabei entspricht ihre Geschwindigkeit exakt der des Zuges. Ihre Bewegungsrichtung ist jedoch entgegengesetzt. In Bezug auf das am Bahnhof liegende Inertialsystem ist sie nicht in Bewegung: Die Person steht. Im Inertialsystem des Zuges führt sie jedoch eine Bewegung aus.
Inertial system
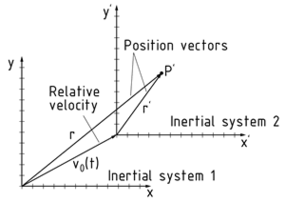
An inertial system is a system of coordinates in which bodies move uniformly in a straight line with no forces acting on them. This behaviour is based on Galileo's law of inertia. Inertia is when a body keeps moving as long as there is no Force acting on it. This inertia is proportional to the body's mass, which can also be considered a point mass.
A point P can be defined using the position vectors of the relevant inertial systems. In the diagram, $\vec{{r}'}$is the position of the point P. It is determined using the Galilean transformation in relation to another inertial system as follows: ${\vec{r}}'=\vec{r}-{{\vec{v}}_{0}}t$. where ${{\vec{v}}_{0}}$ is the relative Velocity and t the time.
It is extremely important to take inertial systems into account in movements. For unambiguous evaluation, they must be considered in relation to a reference system.
Example: A person is moving in a train travelling at a slow speed. This person is moving at exactly the same speed as the train but in the opposite direction. Based on the inertial system of the train station, the person is stationary. Based on the train's inertial system, however, the person is moving.
惯性系
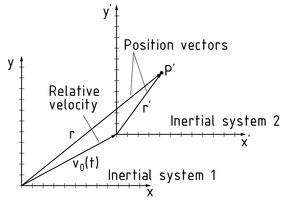
惯性系 指在无外力作用条件下物体匀速直线运动的坐标系。 这一行为遵从伽利略惯性定律。 惯性指无外力作用时,物体会一直保持其运动状态。惯性正比于物体质量,也可理解为质点。
质点 P 可以用惯性系中的位置向量来定义。图中, $\vec{{r}'}$ 是P点的位置。这一位置可以采用伽利略变换得到,公式如下: ${\vec{r}}'=\vec{r}-{{\vec{v}}_{0}}t$ 。 ${{\vec{v}}_{0}}$ 指相对速度, t 指时间。
在运动过程中引入惯性系是非常重要的。为保证计算准确,必须考虑参考系。
例子:一个人在缓慢行驶的火车上运动。 这个人的运动速度和火车的行驶速度相同但方向相反。以火车站作为惯性系,这个人是保持静止的。以火车作为惯性系,这个人是运动的。
两个惯性系的转换
Sistema inercial
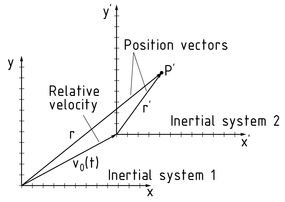
Un sistema inercial es un sistema de coordenadas en el cual los cuerpos se mueven de manera uniforme en una línea recta y ninguna fuerza actúa sobre ellos. Este comportamiento se basa en la ley de inercia de Galileo. Inercia es cuando un cuerpo se mantiene en movimiento mientras que ninguna fuerza actúa sobre él. Esta inercia es proporcional a la masa del cuerpo, la cual también puede ser considerada como masa puntual.
Un punto P puede definirse usando los vectores de posición de los sistemas inerciales relevantes. En el diagrama, $\vec{{r}'}$es la posición del punto P. Se determina usando la transformación de Galileo en relación con otro sistema inercial, como ser: ${\vec{r}}'=\vec{r}-{{\vec{v}}_{0}}t$ . donde ${{\vec{v}}_{0}}$ es la velocidad relativa y t el tiempo.
Es extremadamente importante considerar los sistemas inerciales en los movimientos. Para una evaluación ambigua, estos se deben considerar en relación con un sistema de referencia.
Ejemplo: Una persona se mueve en un tren que viaja a baja velocidad. Esta persona se está moviendo exactamente a la misma velocidad que el tren pero en dirección opuesta. Basada en el sistema inercial de la estación de trenes, la persona está estacionaria. Basada en el sistema inercial del tren, sin embargo, la persona se está moviendo.
Transformación de dos sistemas inerciales
