Torsion
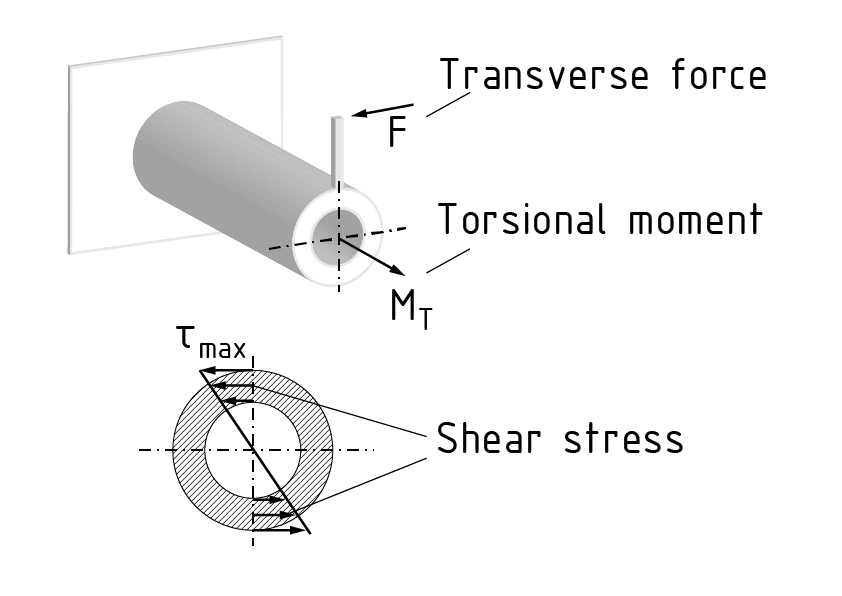
Eine Torsion ist ein Belastungszustand, der durch das Wirken eines Torsionsmomentes MT eine Verdrehung $\vartheta $ hervorruft. Ein Torsionsmoment entsteht z. B. beim Wirken einer Querkraft und eines Hebelarms d.
Die Verformung ist abhängig von der Querschnittgeometrie des tordierten Bauteils. So tritt beispielsweise an Bauteilen mit rundem Querschnitt keine Verwölbung auf. Abhängig von dem wirkenden Torsionsmoment MT , dem werkstoffabhängigen Schubmodul G, der Geometrie des Querschnittes und dem daraus resultierenden Torsionsträgheitsmoment IT ist die Verdrehung pro Längeneinheit $\frac{d\vartheta }{dx}$ berechenbar.
Für Torsionen gilt im Allgemeinen: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$. Das Torsionsträgheitsmoment ${{I}_{T}}$ entspricht bei einem Bauteil mit kreisförmigem Querschnitt dem polaren Flächenträgheitsmoment ${{I}_{P}}$. Im Randbereich dieses Bauteils wirken die größten Schubspannungen $\tau $. Die maximale Schubspannung berechnet sich wie folgt: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{W}_{T}}}$ . Das Torsionswiderstandsmoment WT repräsentiert die Querschnittgeometrie des Bauteils des Bauteils.
-
Beispielsätze:
- The anti-torsion elements are also to be removed as appropriate for this purpose.
- The anti-torsion features of the heavy-duty Hinge in the groove remain effective.
- Use a slotted screwdriver to break off the anti-torsion features.

torsion

Torsión
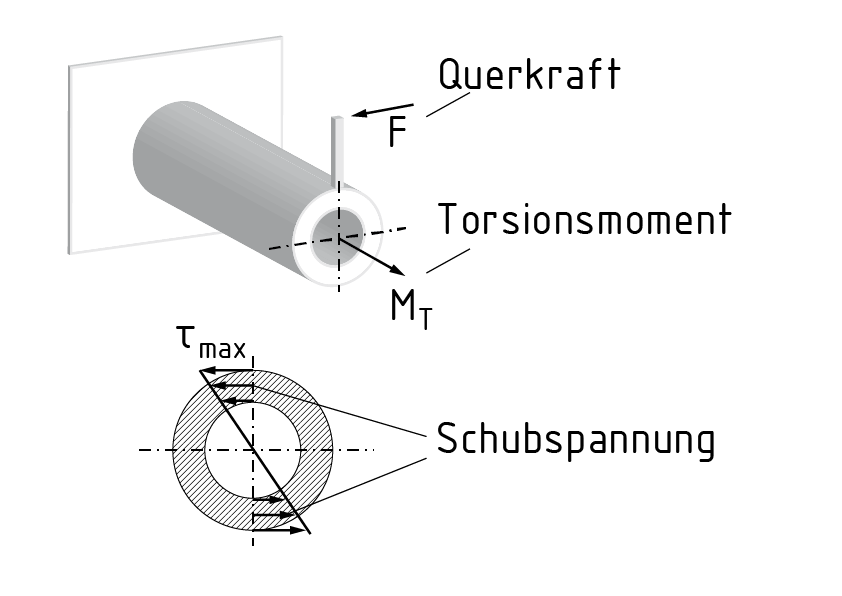
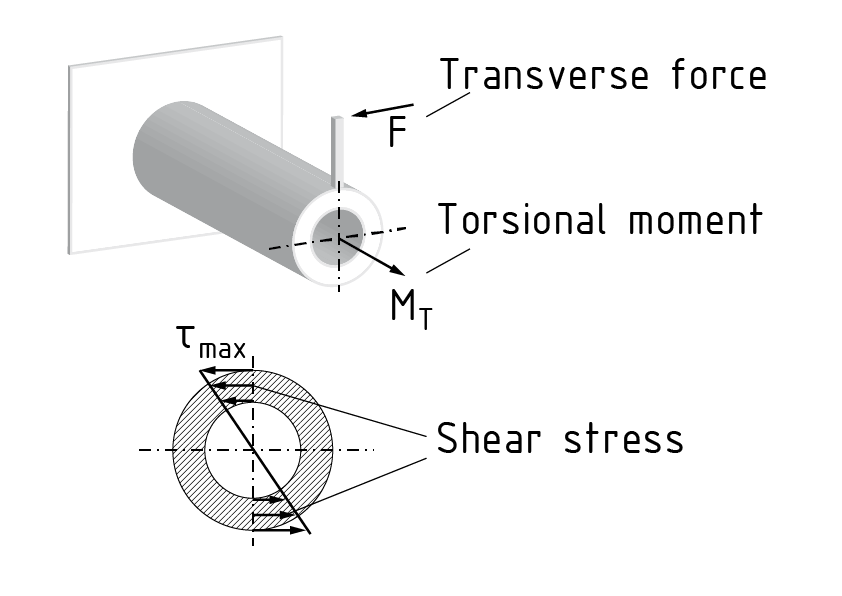
La torsión es un estado de carga que causa un retorcimiento $\vartheta $ debido a la acción de un momento de torsión ${{M}_{T}}$ . Un momento de torsión es creado, por ejemplo, por la acción de una fuerza transversal y un brazo de palanca d.
La deformación depende de la geometría de la sección del componente que se está torciendo. Los componentes con una sección redonda, por ejemplo, no presentan ninguna combadura. La torsión por unidad de longitud $\frac{d\vartheta }{dx}$ puede ser calculada basada en el momento de torsión ${{M}_{T}}$ activo, el módulo de fcorte G dependiente del material, la geometría de la sección y el momento de inercia de torsión ${{I}_{T}}$ resultante.
Lo siguiente aplica generalmente a las torsiones: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$ . En el caso de un componente con una sección circular, el momento de inercia de torsión ${{I}_{T}}$ es equivalente al momento de inercia de área polar ${{I}_{P}}$ . Los esfuerzos de corte más grandes $\tau $ se encuentran en los extremos de este componente. El esfuerzo de corte máximo se calcula de la siguiente manera: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ . El momento de resistencia de torsión ${{R}_{T}}$ representa la geometría de la sección del componente.
Torsión en un componente cilíndrico

Torsión
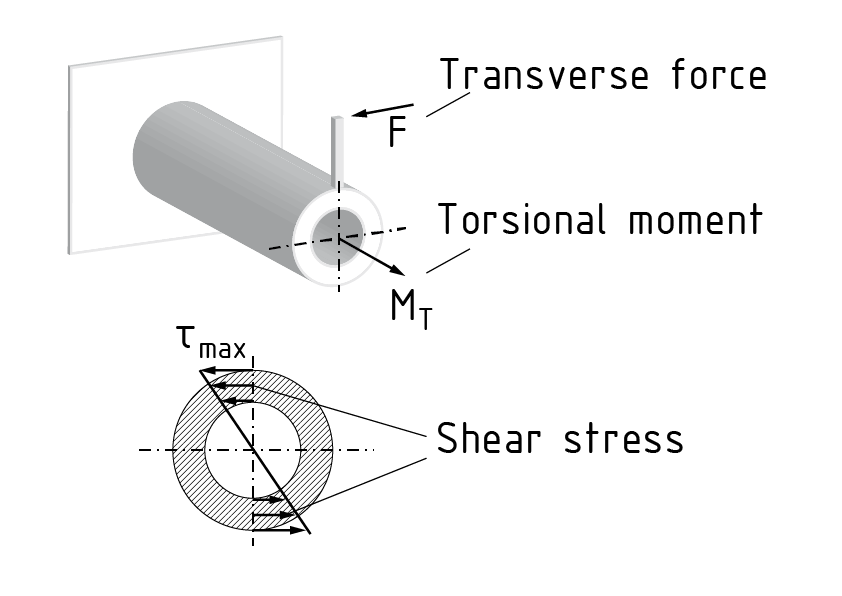
La torsión es un estado de carga que causa un retorcimiento $\vartheta $ debido a la acción de un momento de torsión ${{M}_{T}}$ . Un momento de torsión es creado, por ejemplo, por la acción de una fuerza transversal y un brazo de palanca d.
La deformación depende de la geometría de la sección del componente que se está torciendo. Los componentes con una sección redonda, por ejemplo, no presentan ninguna combadura. La torsión por unidad de longitud $\frac{d\vartheta }{dx}$ puede ser calculada basada en el momento de torsión ${{M}_{T}}$ activo, el módulo de fcorte G dependiente del material, la geometría de la sección y el momento de inercia de torsión ${{I}_{T}}$ resultante.
Lo siguiente aplica generalmente a las torsiones: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$ . En el caso de un componente con una sección circular, el momento de inercia de torsión ${{I}_{T}}$ es equivalente al momento de inercia de área polar ${{I}_{P}}$ . Los esfuerzos de corte más grandes $\tau $ se encuentran en los extremos de este componente. El esfuerzo de corte máximo se calcula de la siguiente manera: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ . El momento de resistencia de torsión ${{R}_{T}}$ representa la geometría de la sección del componente.
Torsión en un componente cilíndrico


扭转