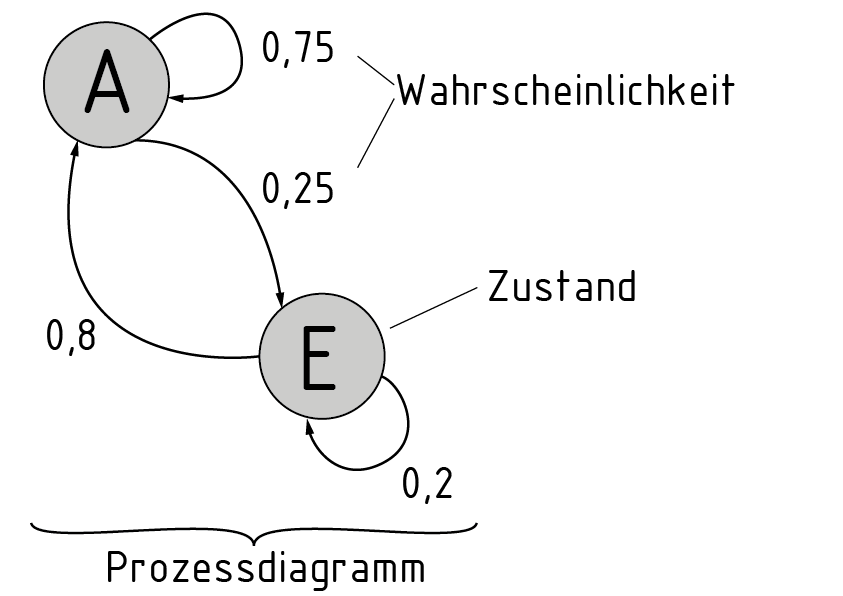
Markow-Kette
Eine Markow-Kette ist ein stochastischer Prozess, mit dem sich die Wahrscheinlichkeiten für das Eintreten bestimmter Zustände bestimmen lässt.
In Form eines Prozessdiagrammes lassen sich die Wahrscheinlichkeiten je nach Zustand und der Beziehung zueinander abbilden. Die möglichen Zustände werden durch Kreise symbolisiert. Die Übergangswahrscheinlichkeit zwischen den Zuständen wird mit Pfeilen und zugehöriger Wahrscheinlichkeit dargestellt.
Eine Übergangsmatrix ist eine alternative Darstellungsform in Matrizenschreibweise. Je Spalte ergibt die Summe der Koeffizienten in der Matrix 1. Durch Multiplikation der Übergangsmatrix mit der Zustandsverteilung wird der nächste eintretende Zustand im Prozess errechnet.
Unterschieden werden verschiedene Arten von Markow-Prozessen:
- stetige
- diskrete, endliche
- diskrete, unendliche
Ein stetiger Markow-Prozess wie der sogenannte Wiener-Prozess besteht aus reellen Zahlen. Ein diskreter, endlicher Markow-Prozess ist z. B. die sogenannte Irrfahrt oder auch Zufallsbewegung, bei der die Zufallsvariablen unabhängig voneinander sind und die Schritte zufällig erfolgen. Wird ein Zustand durch zwei Variablen beschrieben, so ist dies mit einem diskreten, unendlichen Markow-Prozess abzubilden.
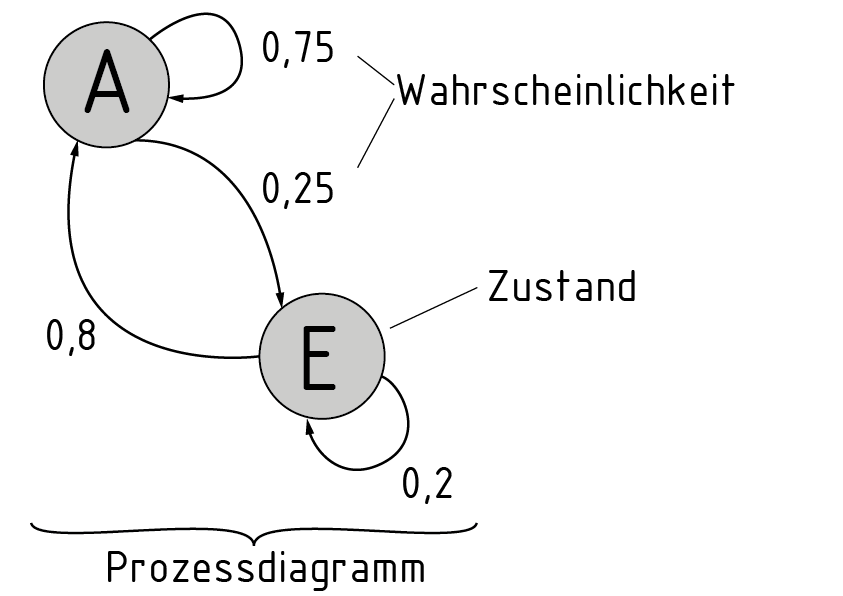

Markov chain

Cadena de Markov
Una cadena de Markov es un proceso estocástico usado para determinar las probabilidades de los estados específicos que se producen.
Las probabilidades pueden mostrarse de acuerdo con su estado y su relación entre sí en forma de diagrama de proceso. Los posibles estados se simbolizan con círculos. La probabilidad de una transición entre estados se indica usando flechas y una probabilidad asociada.
Una matriz de transición es una forma alternativa de representación. La suma de los coeficientes de cada columna en la matriz equivale a 1. El siguiente estado a ocurrir en el proceso se calcula multiplicando la matriz de transición por la distribución de estado.
Existen diferentes tipos de procesos de Markov:
continuo
discreto, finito
discreto, infinito
Un proceso de Markov continuo como el proceso Wiener consiste en números reales. Los procesos de Markov finitos, discretos incluyen el camino aleatorio, donde las variables aleatorias son independientes entre sí y los pasos se realizan de manera aleatoria. Si un estado se describe por dos variables, esto se representa usando un proceso de Markov infinito, discreto.
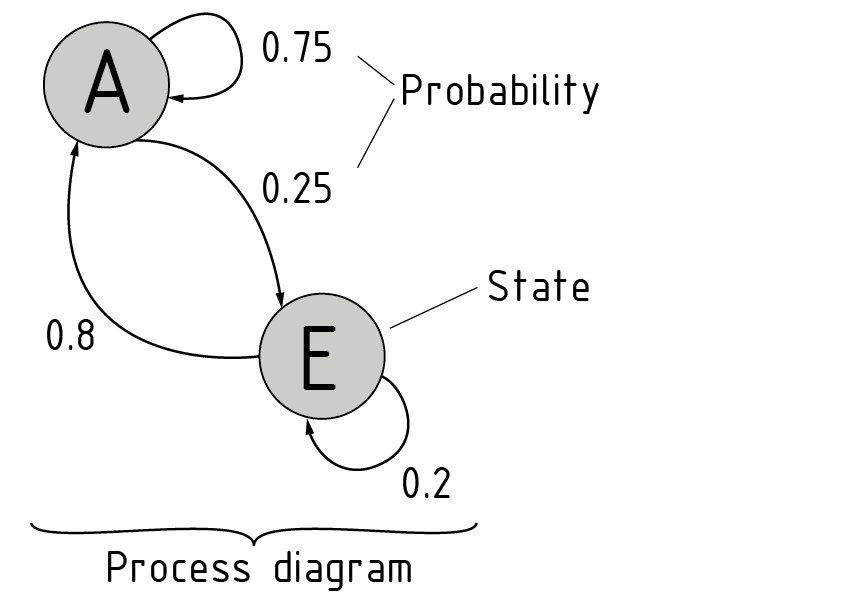
Cadena de Markov en el diagrama de proceso

Cadena de Markov
Una cadena de Markov es un proceso estocástico usado para determinar las probabilidades de los estados específicos que se producen.
Las probabilidades pueden mostrarse de acuerdo con su estado y su relación entre sí en forma de diagrama de proceso. Los posibles estados se simbolizan con círculos. La probabilidad de una transición entre estados se indica usando flechas y una probabilidad asociada.
Una matriz de transición es una forma alternativa de representación. La suma de los coeficientes de cada columna en la matriz equivale a 1. El siguiente estado a ocurrir en el proceso se calcula multiplicando la matriz de transición por la distribución de estado.
Existen diferentes tipos de procesos de Markov:
continuo
discreto, finito
discreto, infinito
Un proceso de Markov continuo como el proceso Wiener consiste en números reales. Los procesos de Markov finitos, discretos incluyen el camino aleatorio, donde las variables aleatorias son independientes entre sí y los pasos se realizan de manera aleatoria. Si un estado se describe por dos variables, esto se representa usando un proceso de Markov infinito, discreto.
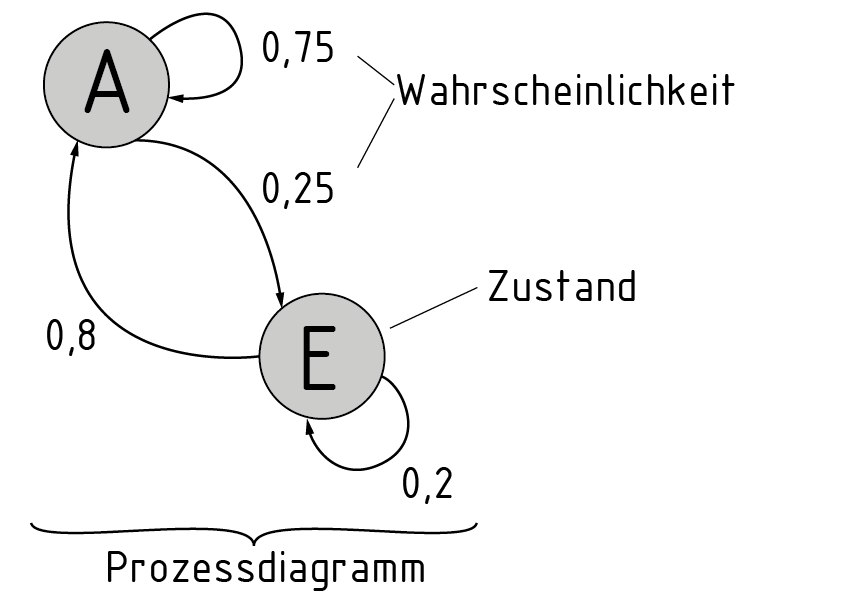
Cadena de Markov en el diagrama de proceso


cadena Markov

马尔可夫链