
Drehbewegung

rotary motion

rotary movement

rotating motion
Description:
Brakes are mainly used to reduce rotating motion, but linear movements can also be slowed through a slight design modification.
-
Example sentences:
- Brakes are mainly used to reduce rotating motion, but linear movements can also be slowed through a slight design modification.

rotation
Description:
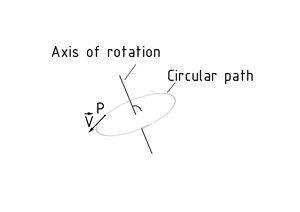
Rotation is the movement of a body on a two-dimensional circular path around an axis of rotation. The plane through which the circular path travels is perpendicular to the axis of rotation. By contrast, the movement of a body in a straight line is referred to as translation. The parameters of rotational movement are angular Velocity $\omega $, Angular acceleration $\alpha $, moment M and angular momentum L. The velocity vector$\vec{v}$ of any point P in the Turning body is tangential to its trajectory. The greater the distance between this point P and the axis of rotation, the larger the tangential velocity $\vec{v}$ that acts on the point. The reason for this is that, during each revolution, a point located closer to the axis of rotation covers a shorter distance ($2\pi $multiplied by the radius) than a point located further away in the same period of time.
-
Example sentences:
- The die head performs the rotational and linear movements.
- Its adjustable frictional moment is consistent regardless of the direction of rotation.
- In the case of a body-fixed system of coordinates, a polhode is used to depict instantaneous centres of rotation.

movimiento rotativo

rotación
Description:
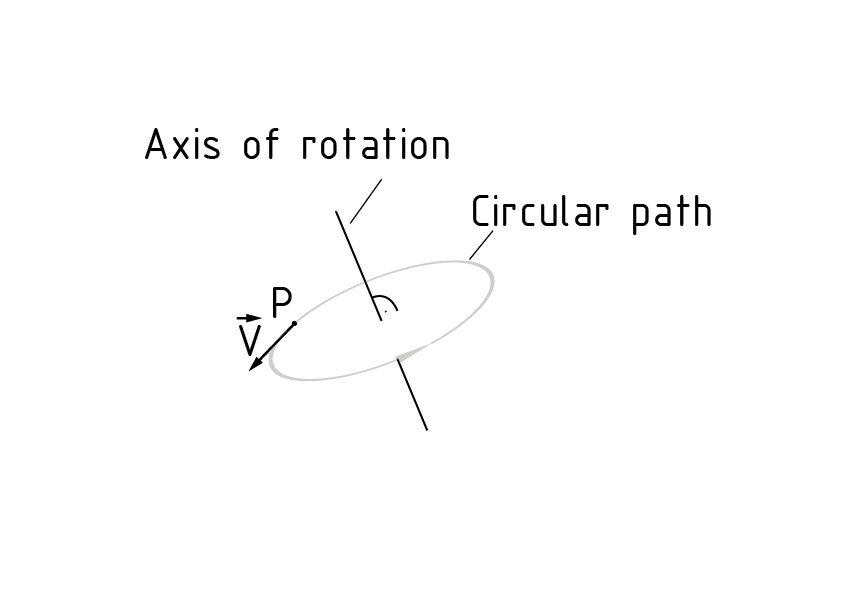
La rotación es el movimiento de un cuerpo en una ruta circular bidimensional alrededor de un eje de rotación. El plano a través del cual la ruta circular viaja es perpendicular al eje de rotación. En contraste, el movimiento de un cuerpo en línea recta es referido como traslación. Los parámetros del movimiento rotacional son la velocidad angular $\omega $, la aceleración angular $\alpha $, el momento M y el momento angular L. El vector de velocidad $\vec{v}$ de cualquier punto P en un cuerpo que gira es tangencial a su trayectoria. Mientras mayor sea la distancia entre este punto P y el eje de rotación, mayor será la velocidad tangencial $\vec{v}$ que actúa en el punto. La razón de esto es que, durante cada revolución, un punto ubicado más cerca del eje de rotación cubre una distancia menor ( $2\pi $ multiplicado por el radio) que un punto ubicado más lejos en el mismo periodo. Eje de rotación durante la rotación

旋转

