Measurement evaluation

Lage der Messwerte - Richtigkeit und Präzision der Messung

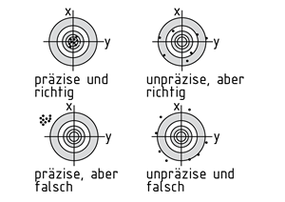
A measurement evaluation is used to find the true value of a measured quantity as accurately as possible. The evaluation tries to compensate for the influence on the result of the measuring inaccuracies that occur with every measurement.

Measuring result = measured value ± measurement uncertainty

The measurement uncertainty indicates the scatter of the measured values. There are two key features that need to be taken into account when performing several measurements.

• Correctness of the measurement: From a statistical perspective, the measured values are distributed uniformly around the true value.
• Precision of the measurement: The measured values lie close together but their mean value may deviate from the true value.

Two methods are used to determine the measurement uncertainty.

• Determining the Standard measurement uncertainty by statistically analysing numerous series of measurements:_x000B_This method is used for series of measurements involving large numbers of measurements. The arithmetic mean is calculated from the values of the individual measurements. Provided there are no systematic errors, this method provides a good estimate of the true value.
• Determining the standard measurement uncertainty using other methods:_x000B_If the measured values can be assumed to be uniformly spread between a defined maximum and minimum (rectangular or continuous uniform distribution), the mean value is calculated using $\bar x = \frac{{{x_{\max }} + {x_{\min }}}}{2}$. The standard measuring inaccuracy is determined as follows: $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {12} }}$._x000B_If the data or other findings lead to the conclusion that the measured values are relatively close to the mean value (triangular distribution), the standard measurement uncertainty is determined as follows: $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {24} }}$.

Messauswertung

Lage der Messwerte - Richtigkeit und Präzision der Messung

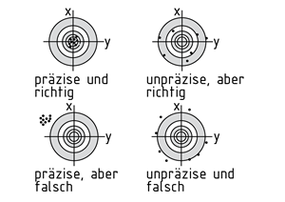
Eine Messauswertung dient dem Ziel, möglichst den wahren Wert einer Messgröße zu finden. Die Messauswertung versucht den Einfluss der bei jeder Messung auftretenden Messungenauigkeiten auf das Messergebnis zu kompensieren.

Messergebnis = Messwert ± Messunsicherheit

Die Messunsicherheit bezeichnet die Streuung der Messwerte. Dabei gibt es zwei wesentliche Eigenschaften, die bei mehreren Messungen beachtet werden sollten.

• Richtigkeit der Messung: Die gemessenen Werte liegen statistisch gleichmäßig um den wahren Wert verteilt.
• Präzision der Messung: Die gemessenen Werte liegen nah zusammen, können im Mittel jedoch vom wahren Wert abweichen.

Die Ermittlung der Messunsicherheit erfolgt durch zwei Methoden.

• Ermittlung der Standardmessunsicherheit durch statistische Analyse von Messreihen:_x000B_Die Methode findet bei Messreihen mit einer großen Anzahl von Messungen Anwendung. Aus den Werten der Einzelmessungen wird das arithmetische Mittel gebildet. Ohne systematische Fehler liefert diese Methode eine gute Schätzung für den wahren Wert.
• Ermittlung der Standardmessunsicherheit mit anderen Verfahren:_x000B_Können die Messwerte zwischen einem definierten Maximum und Minimum als gleichmäßig angenommen werden (Rechteckverteilung), so errechnet sich der Mittelwert $\bar x = \frac{{{x_{\max }} + {x_{\min }}}}{2}$. Die Standardmessunsicherheit bestimmt sich zu $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {12} }}$._x000B_Geben die Daten oder sonstige Erkenntnisse darüber Aufschluss, dass die Messwerte eher beim Mittelwert liegen (Dreieckverteilung), so ergibt sich die Standardmessunsicherheit zu $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {24} }}$.

测量评价

测量值的定位 - 测量的正确性及精确度

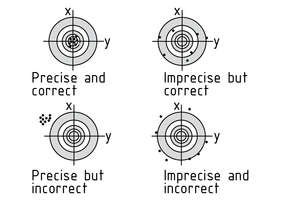
测量评价用于寻找一个与测量值尽可能接近的真值。评价试图补偿每次测量产生的测量不准确结果的影响。

测量结果 = 测量值 ± 测量不确定度

测量不确定度表示测量值的分散情况。进行多次测量时，必须考虑到两个关键特征。

测量的正确性：从统计学的角度来看，所测量的值均匀地围绕真值分布。

测量的精确度：测量值靠近在一起，但其平均值可能偏离真值。

两种方法用于确定测量不确定度。

通过统计分析一系列大量的测量结果，确定标准测量不确定度： 此方法基于大量测量的一系列测量。从单个测量的值计算其算术平均值。只要不存在系统误差，这种方法能够对真值进行很好的估计。

使用其他方法确定标准测量不确定度：如果可以假定测量值被均匀地分布在限定最大值和最小值之间（矩形或连续均匀分布），可以通过 $\bar x = \frac{{{x_{\max }} + {x_{\min }}}}{2}$ 计算其平均值。标准测量不确定度按如下公式确定： $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {12} }}$ .

如果数据或其他结果导致这样的结论：所测量的值与平均值是相对接近的（三角形分布），则标准测量不确定度可以通过公式 $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {24} }}$ 计算。

测量值的定位 - 测量的正确性及精确度

近义词

测量不确定度

测量的正确性

测量的精确度

Evaluación de la medición

Posición de los valores medidos, exactitud y precisión de la medición

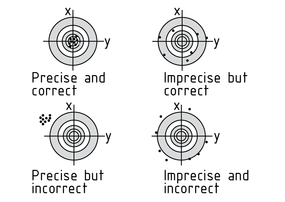
Una evaluación de la medición se usa para determinar el valor cierto de una cantidad medida con la mayor presición posible. La evaluación intenta compensar la influencia en el resultado de las imprecisiones de medición que ocurren con cada medición.

Resultado de medición = valor medido ± incertidumbre de medición

Las incertidumbres de medición indican el nivel de dispersión de los valores medidos. Hay dos características clave que deben ser consideradas cuando se llevan a cabo varias mediciones.

Exactitud de la medición: Desde un punto de vista estadístico, los valores medidos están distribuidos uniformemente alrededor del valor cierto.

Precisión de la medición: Los valores medidos están cerca entre sí, pero el valor medio puede desviarse del valor cierto.

Los dos métodos se usan para determinar la incertidumbre de medición.

Determinación de la incertidumbre de medición estándar al analizar estadísticamente series de medición:Este método se usa para series de mediciones que involucran grandes números de mediciones. La media aritmética se calcula a partir de los valores de las mediciones individuales. Considerando que no hay errores sistemáticos, este método proporciona una buena estimación del valor cierto.

Determinación de la incertidumbre de medición estándar usando otros métodos:Si los valores medidos pueden asumirse como distribuidos uniformemente entre el máximo y mínimo definidos (distribución uniforme rectangular o continua), el valor medio se calcula usando $\bar x = \frac{{{x_{\max }} + {x_{\min }}}}{2}$. La imprecisión de medición estándar se determina de la siguiente manera: $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {12} }}$.Si los datos y otros hallazgos conducen a la conclusión de que los valores medidos están relativamente cerca del valor medio (distribución triangular), la incertidumbre de medición estándar es determinada de la siguiente manera: $u(x) = \frac{{{x_{\max }} - {x_{\min }}}}{{\sqrt {24} }}$.

Posición de los valores medidos, exactitud y precisión de la medición