
Choose one
or multiple languages
0,1,1
- German
- English
- Chinese
- Spanish
Markov chain
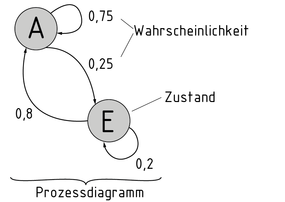
A Markov Chain is a stochastic process used to determine the probabilities of specific states occurring.
The probabilities can be depicted according to their state and their relationship to each other in the form of a process diagram. The possible states are symbolised by circles. The probability of a transition between states is indicated using arrows and an associated probability.
A transition matrix is an alternative form of depiction. The sum of the coefficients for each column in the Matrix equals 1. The next state to occur in the process is calculated by multiplying the transition matrix by the state distribution.
There are a number of different types of Markov processes as follows:
- continuous
- discrete, finite
- discrete, infinite
A continuous Markov process such as the Wiener process consists of real numbers. Discrete, finite Markov processes include random walk, where the random variables are independent of each other and the steps take place on a random basis. If a state is described by two variables, this is depicted using a discrete, infinite Markov process.
Markow-Kette
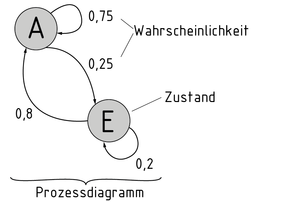
Eine Markow-Kette ist ein stochastischer Prozess, mit dem sich die Wahrscheinlichkeiten für das Eintreten bestimmter Zustände bestimmen lässt.
In Form eines Prozessdiagrammes lassen sich die Wahrscheinlichkeiten je nach Zustand und der Beziehung zueinander abbilden. Die möglichen Zustände werden durch Kreise symbolisiert. Die Übergangswahrscheinlichkeit zwischen den Zuständen wird mit Pfeilen und zugehöriger Wahrscheinlichkeit dargestellt.
Eine Übergangsmatrix ist eine alternative Darstellungsform in Matrizenschreibweise. Je Spalte ergibt die Summe der Koeffizienten in der Matrix 1. Durch Multiplikation der Übergangsmatrix mit der Zustandsverteilung wird der nächste eintretende Zustand im Prozess errechnet.
Unterschieden werden verschiedene Arten von Markow-Prozessen:
- stetige
- diskrete, endliche
- diskrete, unendliche
Ein stetiger Markow-Prozess wie der sogenannte Wiener-Prozess besteht aus reellen Zahlen. Ein diskreter, endlicher Markow-Prozess ist z. B. die sogenannte Irrfahrt oder auch Zufallsbewegung, bei der die Zufallsvariablen unabhängig voneinander sind und die Schritte zufällig erfolgen. Wird ein Zustand durch zwei Variablen beschrieben, so ist dies mit einem diskreten, unendlichen Markow-Prozess abzubilden.
马尔可夫链
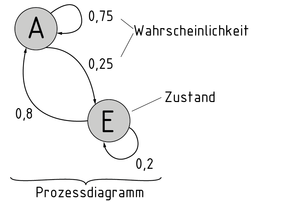
马尔可夫链是一个随机过程,用于计算特定状态的概率。
过程图可以清楚的描述出各个状态的概率及其彼此之间的关系。每个圆圈都表示一个可能的状态。各状态之间的转移概率可用箭头和对应的概率标示出来。
各状态之间的转移概率矩阵可用箭头和对应的概率标示出来。该矩阵每一列的系数之和都等于1。把转移概率矩阵与分布函数相乘,就可计算得到下一状态的概率。
以下是不同类型马尔可夫过程的例子:
连续型
离散型,有限型
离散型,无限型
维纳过程作为一类连续型马尔可夫过程由实数构成。离散、有限型马尔可夫过程包括随机游动,即随机变量彼此独立,步长随机确定。如果一个状态由两个变量描述,即为离散的无限马尔可夫过程。
马尔可夫链过程图
近义词
马尔可夫过程
马尔可夫过程
Cadena de Markov
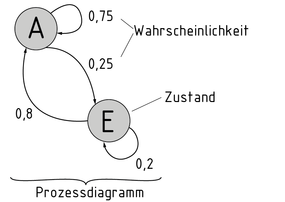
Una cadena de Markov es un proceso estocástico usado para determinar las probabilidades de los estados específicos que se producen.
Las probabilidades pueden mostrarse de acuerdo con su estado y su relación entre sí en forma de diagrama de proceso. Los posibles estados se simbolizan con círculos. La probabilidad de una transición entre estados se indica usando flechas y una probabilidad asociada.
Una matriz de transición es una forma alternativa de representación. La suma de los coeficientes de cada columna en la matriz equivale a 1. El siguiente estado a ocurrir en el proceso se calcula multiplicando la matriz de transición por la distribución de estado.
Existen diferentes tipos de procesos de Markov:
continuo
discreto, finito
discreto, infinito
Un proceso de Markov continuo como el proceso Wiener consiste en números reales. Los procesos de Markov finitos, discretos incluyen el camino aleatorio, donde las variables aleatorias son independientes entre sí y los pasos se realizan de manera aleatoria. Si un estado se describe por dos variables, esto se representa usando un proceso de Markov infinito, discreto.
Cadena de Markov en el diagrama de proceso
