
Choose one
or multiple languages
0,1,1
- German
- English
- Chinese
- Spanish
Acceleration
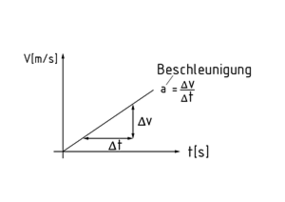
Acceleration a is the change in Velocity v over time t. As a result, it is the first derivation of velocity $a=\frac{dv}{dt}$ and the second derivation of the path over the time.
It is a Vector quantity that exhibits a specific direction and a specific magnitude at each point. A drop in the velocity of a body over time is referred to as deceleration. The acceleration vector $\vec{a}$ is negative in the case of deceleration and positive in the case of acceleration.
- In the case of a uniformly accelerated motion, acceleration is constant (a = const.). Path s applied over time t is described by a parabola. Velocity v exhibits a linear increase over time.
- A uniform motion does not experience any acceleration (a = 0), as its velocity v is constant. It is also referred to as uniform translation or uniform, straight-line motion.
Beschleunigung
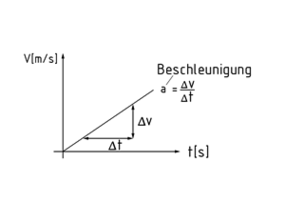
Die Beschleunigung a ist die zeitliche Änderung der Geschwindigkeit v über die Zeit t. Sie ist somit die erste Ableitung der Geschwindigkeit $a=\frac{dv}{dt}$ und die zweite Ableitung des Weges über die Zeit.
Sie ist eine vektorielle Größe, die in jedem Punkt der Bewegung eine bestimmte Richtung und einen bestimmten Betrag aufweist. Die Verminderung der Geschwindigkeit eines Körpers über die Zeit wird Verzögerung genannt. Der Beschleunigungsvektor $\vec{a}$ ist für eine Verzögerung negativ und für eine Beschleunigung positiv gerichtet.
- Bei einer gleichmäßig beschleunigten Bewegung ist die Beschleunigung konstant (a = konst.). Der Weg s aufgetragen über die Zeit t wird durch eine Parabel beschrieben. Der Verlauf der Geschwindigkeit v über die Zeit ist linear ansteigend.
- Eine gleichförmige Bewegung erfährt keine Beschleunigung (a = 0), da ihre Geschwindigkeit v konstant ist. Sie wird auch als gleichförmige Translation oder gleichförmige, geradlinige Bewegung bezeichnet.
加速度
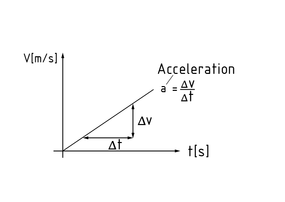
加速度a是指速度v随时间t的变化情况。所以它既是速度对时间的一阶导数 $a=\frac{\Delta v}{\Delta t}$ 也是位移对时间的二阶导数。
加速度是一个矢量,在每一点有特定的大小和方向。速度随时间的增加而减小的现象称为减速。在减速运动中加速度矢量 $\vec{a}$ 为负值,在加速运动中加速度矢量为正值。
在匀加速运动中,加速度为一个常数(a = 常数)。路程s和时间t的关系可由抛物线形式表示,速度v随时间线性增加。
在匀速运动中由于速度v是固定值,所以不存在加速度 (a = 0) 。匀速运动也被称为匀速平移或匀速直线运动。
速度-时间图中的固定加速度
Aceleración
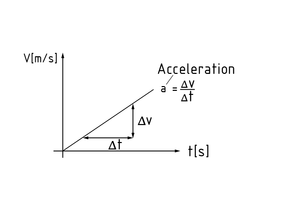
La aceleración a es el cambio en la velocidad v con el tiempo t. Como resultado, es la primera derivación de velocidad $a=\frac{\Delta v}{\Delta t}$ y la segunda derivación de la ruta con el tiempo.
Es una cantidad vectorial que muestra una dirección específica y una magnitud específica en cada punto. Una disminución en la velocidad de un cuerpo con el tiempo es referida como una desaceleración. El vector de aceleración $\vec{a}$ es negativo en el caso de la desaceleración y positivo en el caso de la aceleración.
En el caso de un movimiento uniformemente acelerado, la aceleración es constante (a = const.). La ruta s aplicada con el tiempo t se describe como una parábola. La velocidad v presenta un incremento lineal con el tiempo.
Un movimiento uniforme no experimenta ninguna aceleración (a = 0), ya que su velocidad v es constante. También es referido como translación uniforme o movimiento recto uniforme.
Aceleración constante en un diagrama velocidad-tiempo
