
Fourier-Analyse
Die Fourier-Analyse beschäftigt sich mit den Fourierreihen und -integralen. Eine Fourierreihe ist eine Reihenentwicklung einer Funktion in einer Funktionsreihe aus Kosinus- und Sinus-Funktionen. Sie ist abschnittsweise stetig und verläuft periodisch.
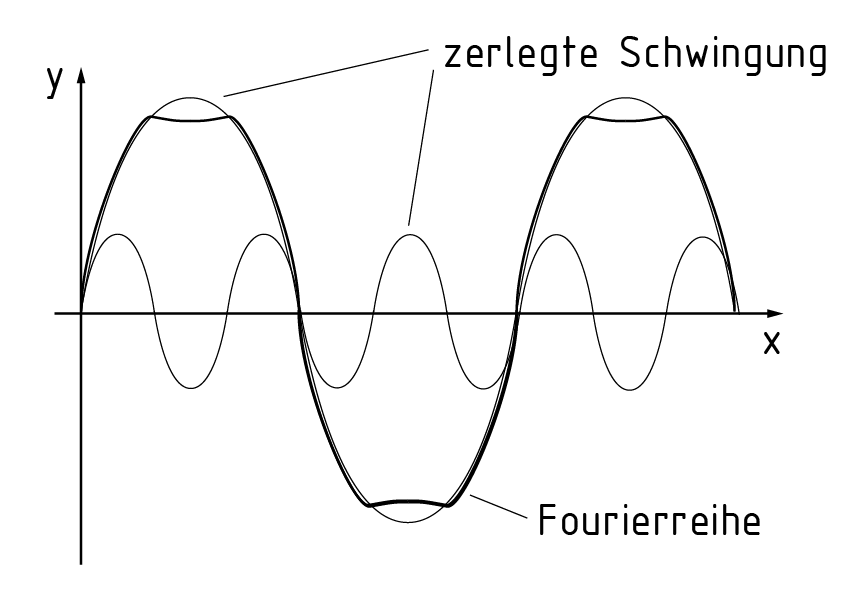
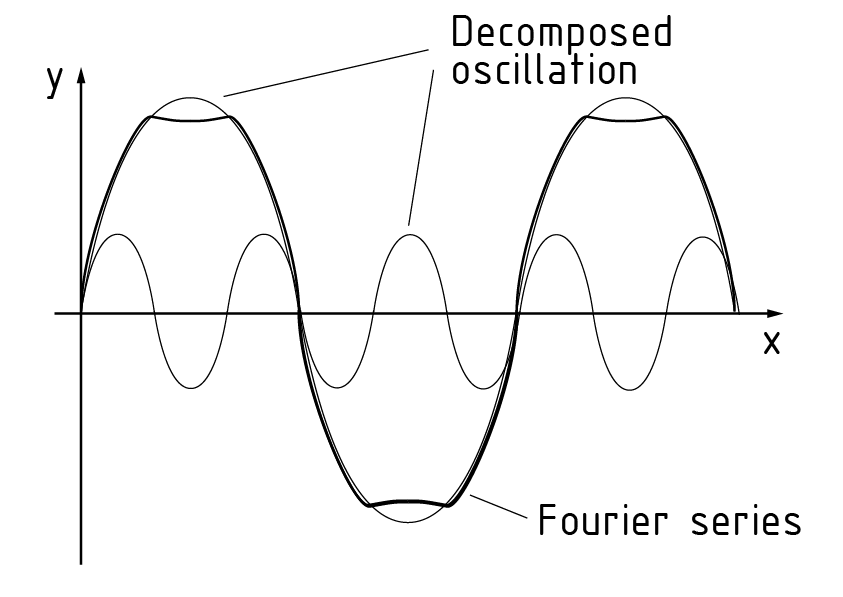
Wird eine Fourierreihe in die durch die trigonometrischen Basisfunktionen dargestellten Schwingungen zerlegt, so wird von Fourier-Analyse gesprochen. Im Bild ist ein Graph dargestellt, der durch eine Fourier-Analyse mit zwei Schwingungen dargestellt wird.
Aufgebaut ist eine Fourierreihe wie folgt:
Das Intervall der Funktion liegt zwischen $-\pi $ und $\pi $. Die Koeffizienten${{a}_{0}}$, ${{a}_{n}}$ und ${{b}_{n}}$ sind zu bestimmen. ${{a}_{n}}$ und ${{b}_{n}}$sind die sog. Fourierkoeffizienten.

Fourier analysis

análisis de Fourier

傅立叶分析

傅里叶分析
傅里叶分析主要研究傅里叶级数和傅里叶积分。傅里叶级数可将一个函数展开成余弦与正弦函数的级数形式。它是分段连续的,且是周期函数。
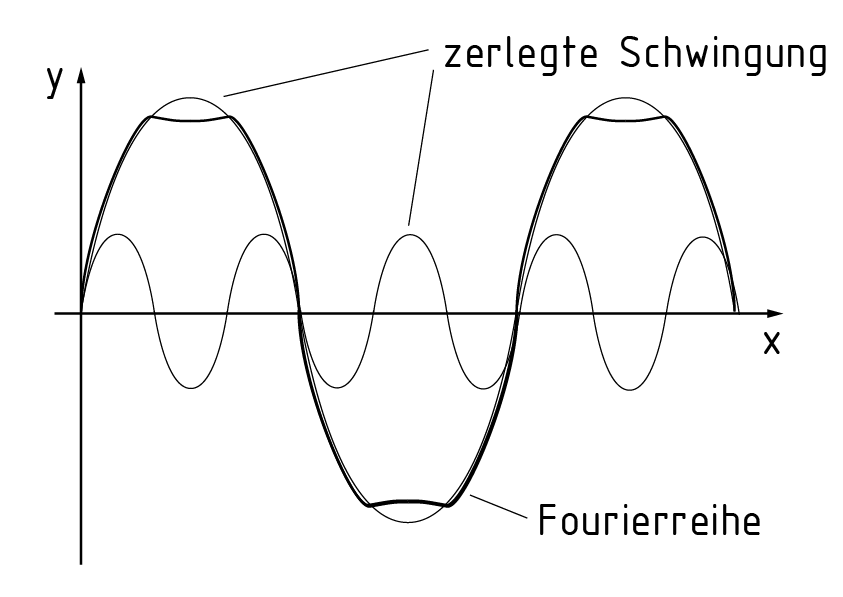
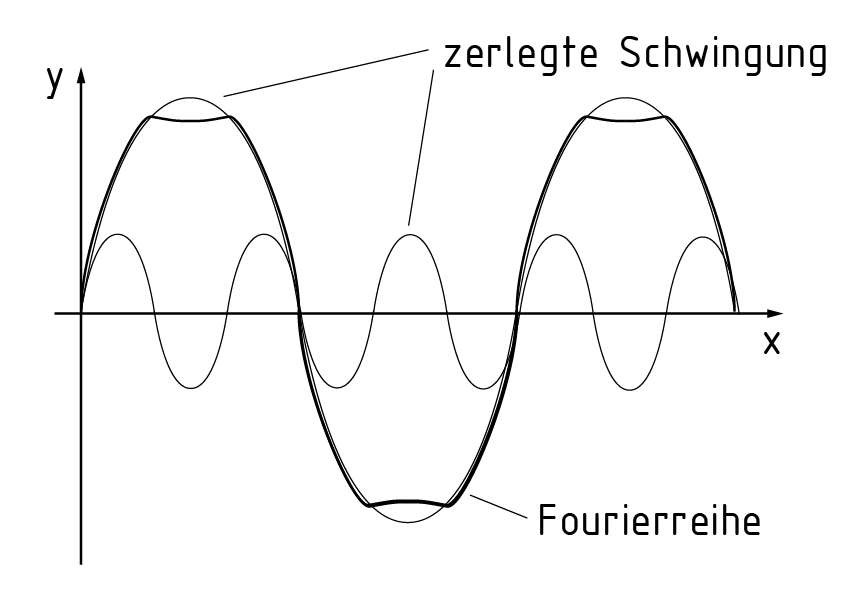
傅里叶分析将傅里叶级数分解成由三角函数表达的震荡。右图呈现了带有两组震荡的傅里叶分析图像。
傅里叶级数有如下结构:
$f(x)=\frac{{{a}_{0}}}{2}+\sum\limits_{n=1}^{\infty }{[{{a}_{n}}\cos (nx)+{{b}_{n}}\sin (nx)]}$
函数的定义区间介于 $-\pi $ 和 $\pi $。系数 ${{a}_{0}}$, ${{a}_{n}}$ 和 ${{b}_{n}}$ 需要确定。 ${{a}_{n}}$ 和 ${{b}_{n}}$ 叫做傅里叶系数。
利用傅里叶分析进行分解
近义词
经典调和分析
傅里叶级数
傅里叶系数

傅里叶分析
傅里叶分析主要研究傅里叶级数和傅里叶积分。傅里叶级数可将一个函数展开成余弦与正弦函数的级数形式。它是分段连续的,且是周期函数。
傅里叶分析将傅里叶级数分解成由三角函数表达的震荡。右图呈现了带有两组震荡的傅里叶分析图像。
傅里叶级数有如下结构:
$f(x)=\frac{{{a}_{0}}}{2}+\sum\limits_{n=1}^{\infty }{[{{a}_{n}}\cos (nx)+{{b}_{n}}\sin (nx)]}$
函数的定义区间介于 $-\pi $ 和 $\pi $。系数 ${{a}_{0}}$, ${{a}_{n}}$ 和 ${{b}_{n}}$ 需要确定。 ${{a}_{n}}$ 和 ${{b}_{n}}$ 叫做傅里叶系数。
利用傅里叶分析进行分解
近义词
经典调和分析
傅里叶级数
傅里叶系数

