
Ebene Bewegung in Polarkoordinaten
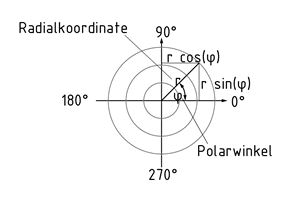
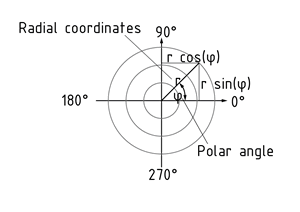
Als Polarkoordinaten wird ein zweidimensionales Koordinatensystem bezeichnet, in dem die Position eines Punktes durch einen Winkel $\varphi $ und den Abstand r vom Ursprung des Koordinatensystems angegeben wird.
Der Abstand r nennt sich Radialkoordinate. Die Winkelkoordinate $\varphi $ (auch Polarwinkel) gibt darüber Auskunft, um wieviel Grad ein Punkt in mathematisch positiver Richtung (linksdrehend) von der Polarachse entfernt ist.
In Polarkoordinaten ausgedrückte Bewegungen werden durch ihre Geschwindigkeitskomponenten angegeben. Diese Zerlegung in Komponenten wird in radialer und dazu senkrechter Richtung durchgeführt. Der Geschwindigkeitsvektor$\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ setzt sich wie folgt zusammen: \[\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }}\] mit ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ und ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$

planar motion in polar coordinates

movimiento plano en coordinadas polares

在极坐标内的平面运动

极坐标中的平面运动
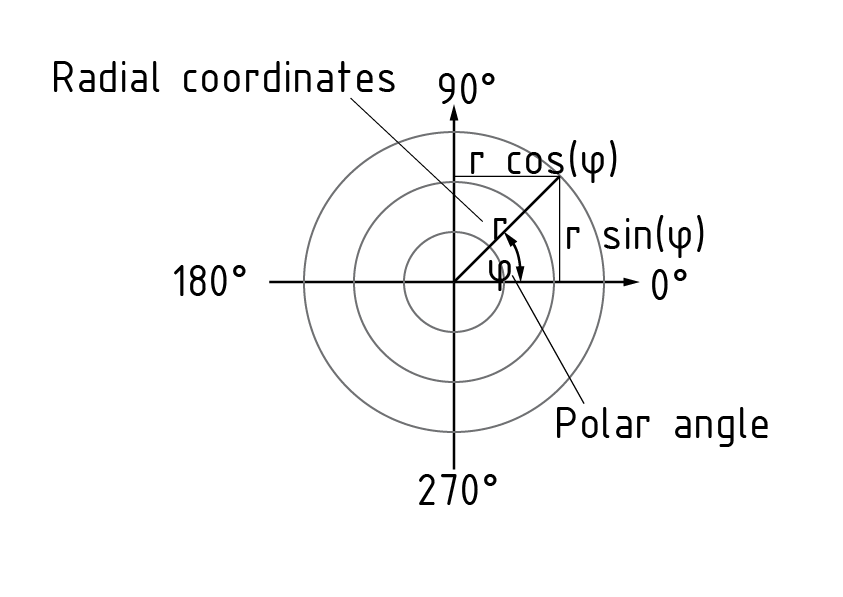
极坐标系是一个二维坐标系,在该坐标系中任意一点都可以用角度 $\varphi $ 和与坐标系原点间的距离r来表示
径向坐标指距离r。角坐标(也称为极角) $\varphi $ 为一点以数学正方向(逆时针)绕极轴旋转的角度。
极坐标中物体的运动可由其速度分量表示。速度可在径向和法向进行分解。速度矢量 $\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ 包括以下分量:$\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }}$ 在 ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ 和 ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$
径向坐标和角坐标

极坐标中的平面运动
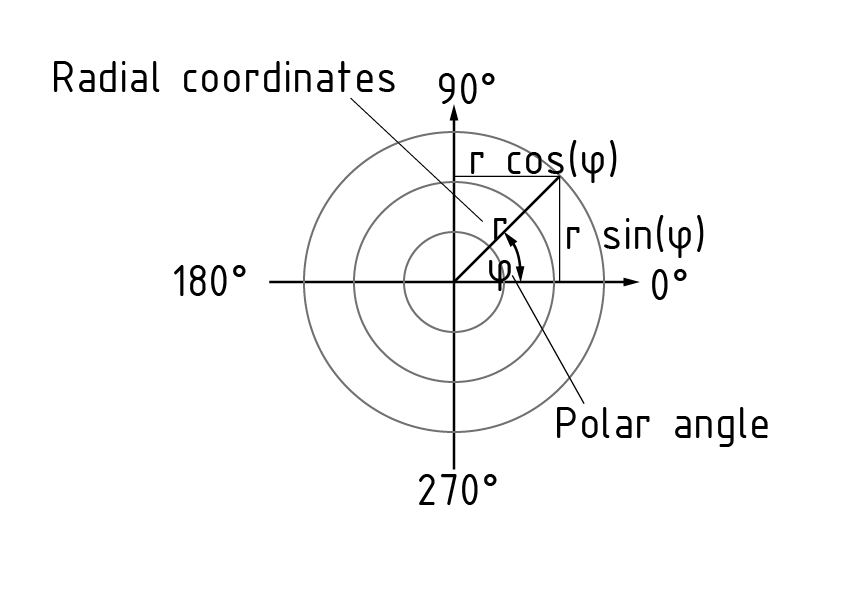
极坐标系是一个二维坐标系,在该坐标系中任意一点都可以用角度 $\varphi $ 和与坐标系原点间的距离r来表示
径向坐标指距离r。角坐标(也称为极角) $\varphi $ 为一点以数学正方向(逆时针)绕极轴旋转的角度。
极坐标中物体的运动可由其速度分量表示。速度可在径向和法向进行分解。速度矢量 $\overset{\cdot }{\mathop{\overrightarrow{r}}}\,$ 包括以下分量:$\overset{\cdot }{\mathop{\overrightarrow{r}}}\,=\dot{r}{{\overrightarrow{e}}_{r}}+r\dot{\varphi }{{\overrightarrow{e}}_{\varphi }}$ 在 ${{\overrightarrow{e}}_{r}}=(\cos (\varphi ),\sin (\varphi ))$ 和 ${{\overrightarrow{e}}_{\varphi }}=(-sin(\varphi ),cos(\varphi ))$
径向坐标和角坐标

