Statische Bestimmtheit
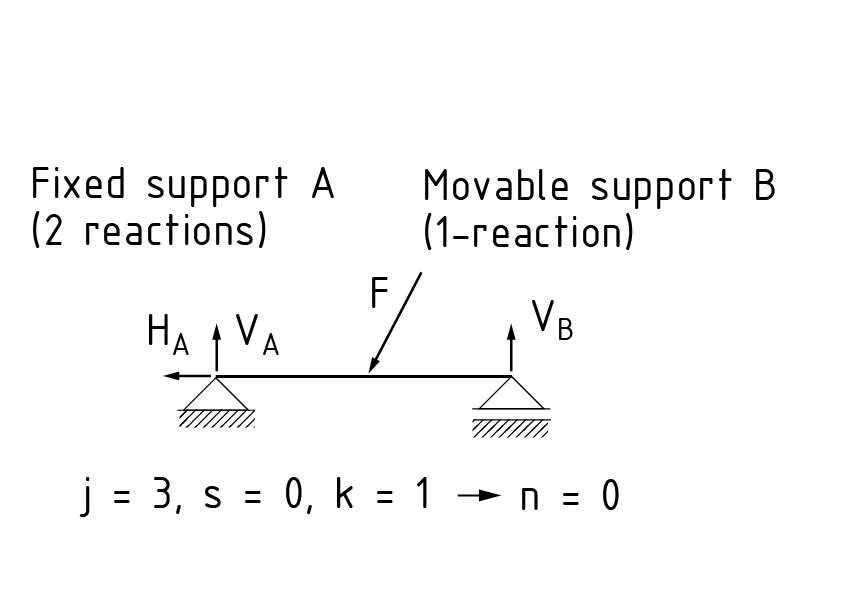
Die statische Bestimmtheit eines statischen Systems ist bei der gleichen Anzahl von Freiheitsgraden wie Lagerreaktionen gegeben. Aus den Gleichgewichtsbedingungen der äußeren Belastungen sind dann die Lagerreaktionen errechenbar.
Im dreidimensionalen Raum gelten sechs Gleichgewichtsbedingungen. Die ersten drei beschreiben die Summe aller Kräfte in die Raumrichtung (x, y, z). Die weiteren drei Gleichungen beschreiben die Summe der Momente um die drei Raumachsen. Alle Gleichungen ergeben null.
Der Grad n der statischen Unbestimmtheit errechnet sich durch:
$n=j+s-6k$ (dreidimensional) bzw. $n=j+s-3k$ (zweidimensional)
Das j ist gleich der Summe aller Wertigkeiten der Lager, s entspricht der Summe aller Wertigkeiten der Verbindungen und k ist die Anzahl der freizuschneidenden Körper.
Liegt ein Fachwerk mit einer Anzahl von z Gelenken, s Stäben und a Auflagereaktionen vor, so lässt sich der Grad der Unbestimmtheit wie folgt berechnen: $n=a+s-2s$
Bei n = 0 liegt ein statisch bestimmtes System vor.
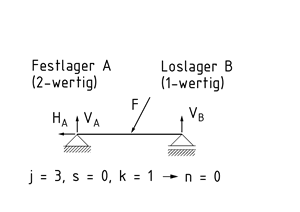
-
Beispielsätze:
- Die statische Bestimmtheit eines statischen Systems ist bei der gleichen Anzahl von Freiheitsgraden wie Lagerreaktionen gegeben.

static determinacy
-
Example sentences:
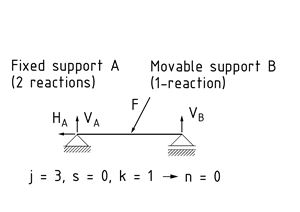
- A static system is said to exhibit static determinacy when it has the same number of degrees of freedom as support reactions.

Determinación estática
Se dice que un sistema estático presenta una determinación estática cuando tiene el mismo número de grados de libertad que de reacciones de soporte. Las reacciones de soporte pueden calcularse sobre la base de las condiciones de equilibrio de las cargas externas.
Existen seis condiciones de equilibrio en un espacio tridimensional. Las primeras tres describen la suma total de todas las fuerzas en las tres dimensiones (x, y, z). Las otras tres ecuaciones describen la suma total de los momentos alrededor de los tres ejes espaciales. Todas las ecuaciones dan como resultado cero.
El grado n de indeterminación estática se calcula del siguiente modo:
$n=j+s-6k$ (tridimensional) o $n=j+s-3k$ (bidimensional)
j es la suma total de todas las reacciones de los soportes (valencia), s es la suma total de todas las reacciones de las conexiones (valencia), y k es el número de cuerpos a ser modelados en un diagrama de cuerpo libre.
Si consideramos una armadura con un número z de uniones, s miembros y a fuerzas de soporte, el grado de indeterminación se calcula del siguiente modo: $n=a+s-2s$
Si n = 0, la armadura presenta determinación estática.
Un sistema estáticamente determinado

Determinación estática
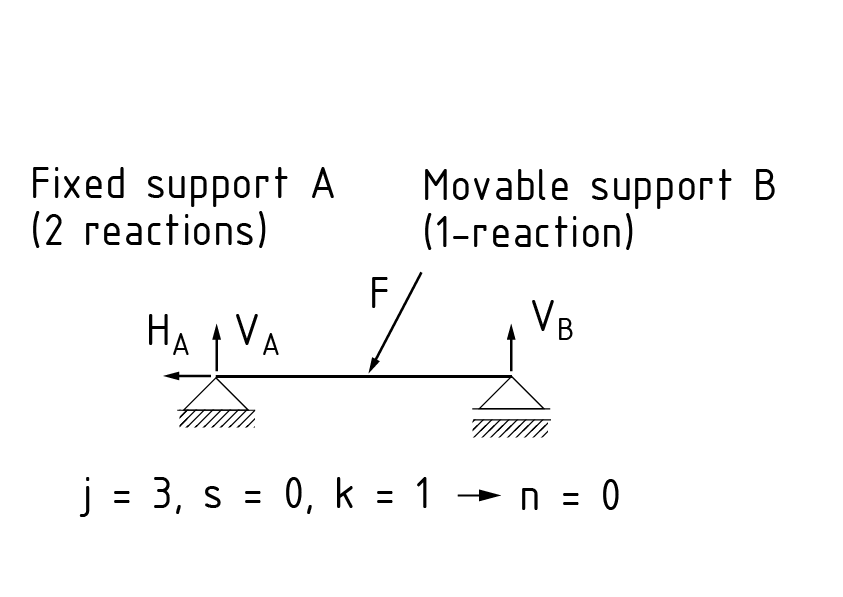
Se dice que un sistema estático presenta una determinación estática cuando tiene el mismo número de grados de libertad que de reacciones de soporte. Las reacciones de soporte pueden calcularse sobre la base de las condiciones de equilibrio de las cargas externas.
Existen seis condiciones de equilibrio en un espacio tridimensional. Las primeras tres describen la suma total de todas las fuerzas en las tres dimensiones (x, y, z). Las otras tres ecuaciones describen la suma total de los momentos alrededor de los tres ejes espaciales. Todas las ecuaciones dan como resultado cero.
El grado n de indeterminación estática se calcula del siguiente modo:
$n=j+s-6k$ (tridimensional) o $n=j+s-3k$ (bidimensional)
j es la suma total de todas las reacciones de los soportes (valencia), s es la suma total de todas las reacciones de las conexiones (valencia), y k es el número de cuerpos a ser modelados en un diagrama de cuerpo libre.
Si consideramos una armadura con un número z de uniones, s miembros y a fuerzas de soporte, el grado de indeterminación se calcula del siguiente modo: $n=a+s-2s$
Si n = 0, la armadura presenta determinación estática.
Un sistema estáticamente determinado


determinancia estática

静定性