Deutsch

Komplexe Zahl (Feminin)

Beschreibung:

Eine komplexe Zahl $z$ ist eine Zahl, die aus einem Imaginärteil $\operatorname{Im}(z)=b$ und einem Realteil $\operatorname{Re}(z)=a$besteht. Komplexe Zahlen erweitern den Bereich der reellen Zahlen durch Einführung einer imaginären Einheit$i$. Es gilt: ${{i}^{2}}=-1$.

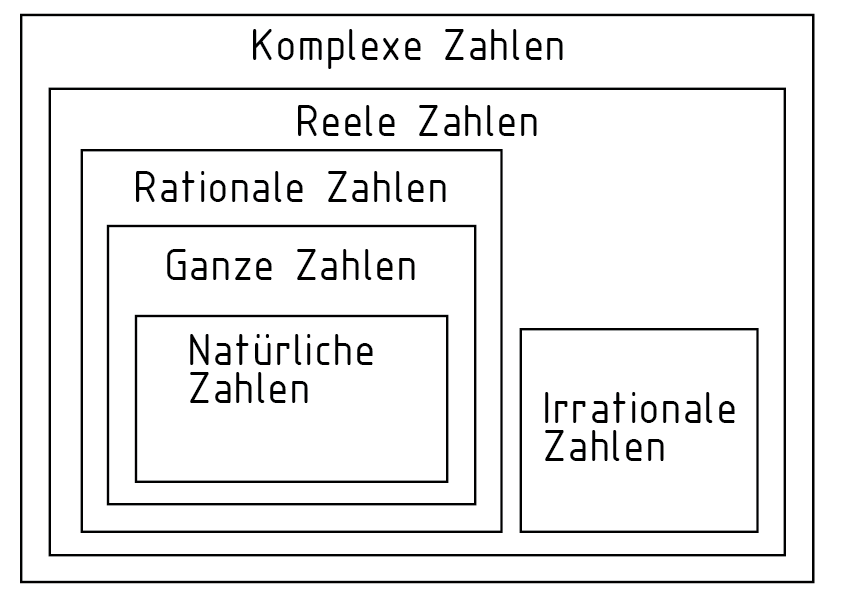
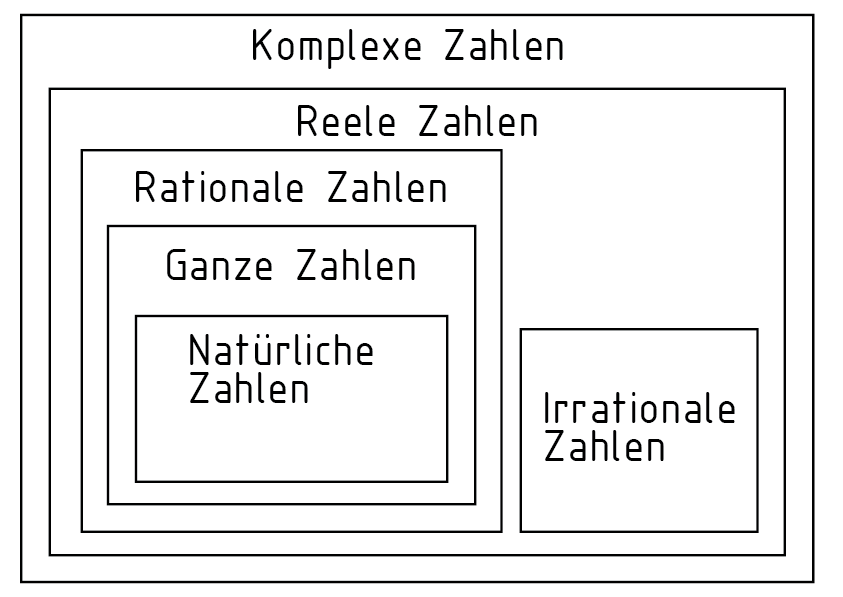
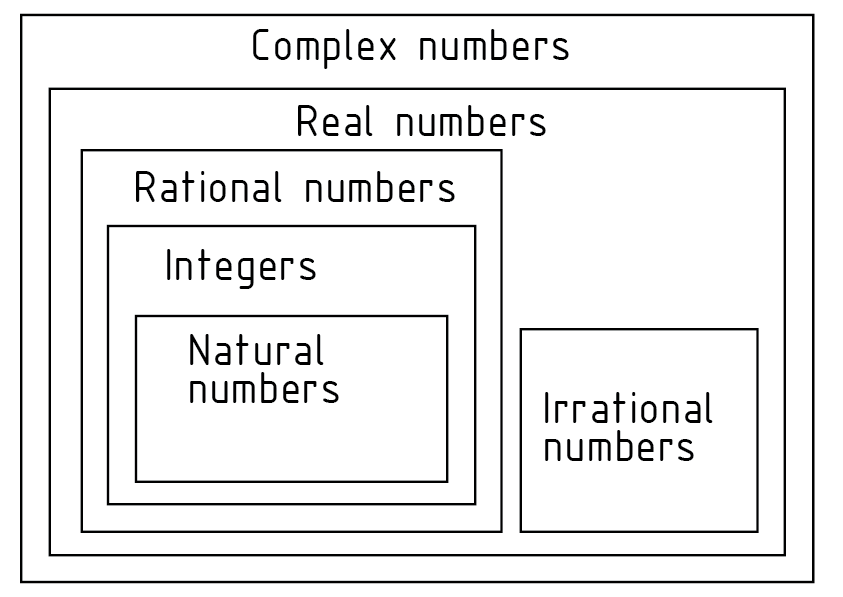
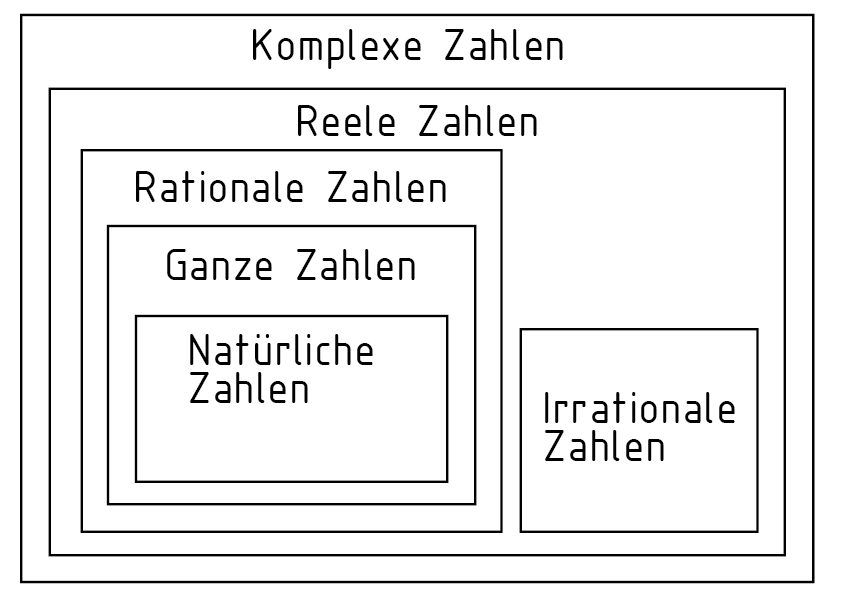
Die Menge der komplexen Zahlen $\mathbb{C}$, in der alle Zahlenmengen enthalten sind, entspricht dem zweidimensionalen Vektorraum der reellen Zahlen ${{\mathbb{R}}^{2}}$. Abgebildet in einer sogenannten gaußschen Zahlenebene ist der Betrag einer komplexen Zahl berechenbar. Dabei wird die komplexe Zahl als Vektor in einem kartesischen Koordinatensystem aufgetragen. Die Abszisse steht in diesem für den Realteil und die Ordinate für den Imaginärteil der komplexen Zahl.

Komplexe Zahlen können weder als positiv noch als negativ bezeichnet werden. Eine komplexe Zahl, die - abgesehen von dem Vorzeichen ihres Imaginärteils - einer anderen komplexen Zahl entspricht, heißt konjungiert-komplexe Zahl.

Nur durch komplexe Zahlen können Gleichungen gelöst werden, bei denen das Quadrat einer Variablen eine negative Zahl ergibt. Die Menge der komplexen Zahlen ist eine Erweiterung zu den reellen Zahlen.

Zahlenmengen - komplexe Zahlen
Zahlenmengen - komplexe Zahlen
English

complex number (Neutrum)

Description: A complex number $z$ is a number comprising an imaginary part $\operatorname{Im}(z)=b$ and a real part $\operatorname{Re}(z)=a$. Complex numbers extend the domain of real numbers by introducing an imaginary unit $i$ where ${{i}^{2}}=-1$. The set of complex numbers $\mathbb{C}$, which includes all sets of numbers, corresponds to the two-dimensional Vector space of the real numbers ${{\mathbb{R}}^{2}}$. The value of a complex number can be calculated using an Argand diagram by plotting it as a vector in a Cartesian coordinate system in which the x-coordinate represents the real part and the y-coordinate the imaginary part. Complex numbers cannot be designated as either positive or negative. A complex number that is the same as another complex number except for the +/- sign of its imaginary part is called a conjugate complex number. Equations in which the square of a variable is negative can only be solved using complex numbers. The set of complex numbers extends the domain of real numbers.
Sets of numbers - complex numbers
Sets of numbers - complex numbers
Spanisch

número complejo (Neutrum)

Description: Un número complejo $z$ es un número que comprende una parte imaginaria $\operatorname{Im}(z)=b$ y una parte real $\operatorname{Re}(z)=a$ . Los números complejos extienden el dominio de los números reales al introducir una unidad imaginaria $i$ donde ${{i}^{2}}=-1$ . El conjunto de números complejos $\mathbb{C}$ , el cual incluye todos los conjuntos numéricos, corresponde al espacio vectorial bidimensional de los números reales ${{\mathbb{R}}^{2}}$ . El valor de un número complejo puede ser calculado usando un diagrama de Argand trazado como vector en el sistema de coordenadas cartesiano, en el cual la coordenada x representa la parte real y la coordenada y la parte imaginaria. Los números complejos no pueden ser designados como positivos o negativos. Un número complejo igual a otro número complejo excepto por el signo +/- de su parte imaginaria se llama número complejo conjugado. Las ecuaciones en las cuales el cuadrado de una variable es negativo solo pueden resolverse usando números complejos. El conjunto de números complejos extiende el dominio de los números reales. Conjunto de números - números complejos
Conjunto de números - números complejos
Conjunto de números - números complejos
Chinesisch

复数 (Neutrum)

Description: 复数 $z$ 由虚部 $\operatorname{Im}(z)=b$ 实部 $\operatorname{Re}(z)=a$ 构成。把虚部单位 $i$ 引入到实数集后，复数扩大了实数集，其中 ${{i}^{2}}=-1$。 复数集 $\mathbb{C}$ 包含所有数集，与之相对应的是二维向量空间 ${{\mathbb{R}}^{2}}$。 复数的值可以利用阿干特图计算，把复数看做向量绘制在直角坐标系中，x轴代表实部，y轴代表虚部。 复数没有正负之分。两个实部相等，虚部互为相反数的向量称为共轭复数。 如果一个方程中某个变量的平方是负数，则只能用复数解决。实数集是复数集的子集。 数集-复数
数集-复数
数集-复数