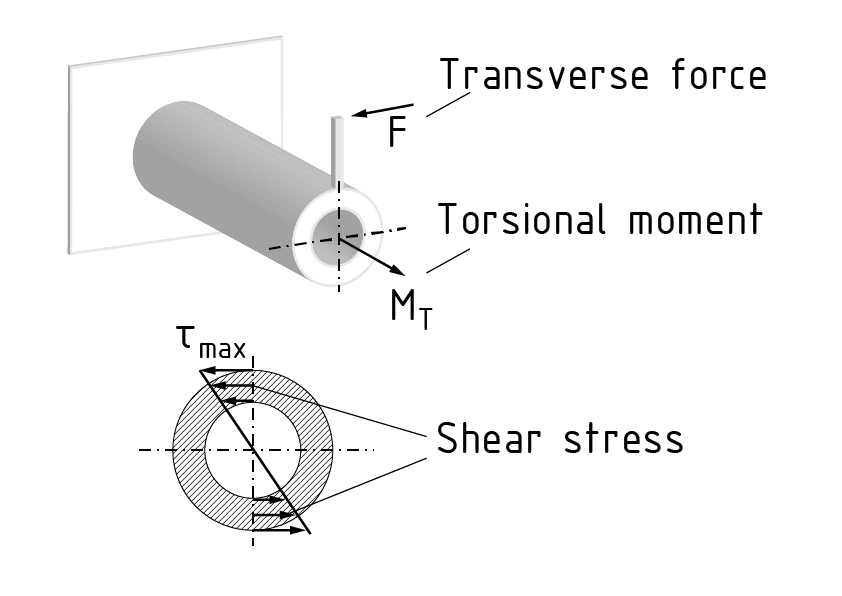
Drehbeanspruchung

torsion
Description:
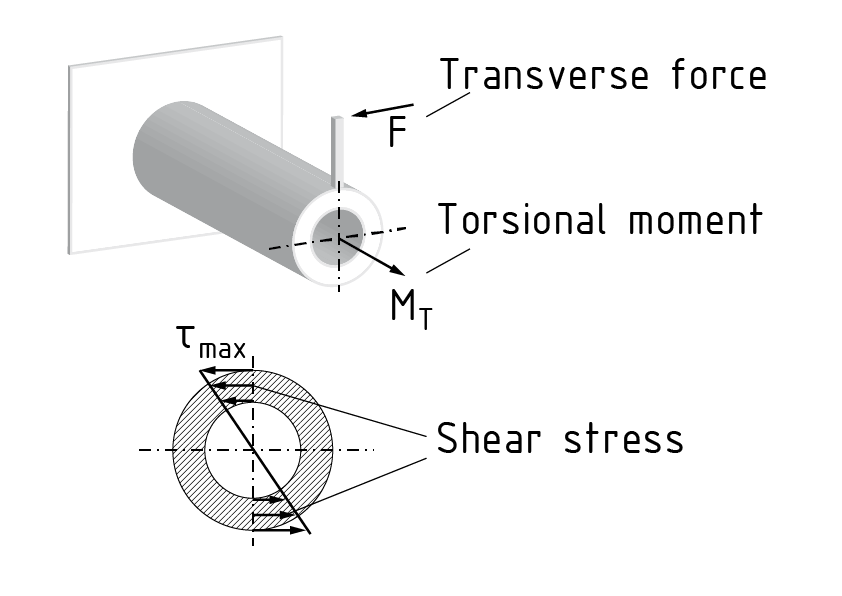
Torsion is a load state that causes twisting $\vartheta $ due to the action of a torsional moment MT. A torsional moment is created, for example, by the action of a transverse Force and a lever arm d. The deformation depends on the cross-sectional geometry of the component being twisted. Components with a round cross-section, for example, do not exhibit any warping. The twisting per unit of length $\frac{d\vartheta }{dx}$ can be calculated based on the active torsional moment MT , the material-dependent shear modulus G, the cross-sectional geometry and the resultant torsional moment of inertia IT. The following generally applies to torsions: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$. In the case of a component with a circular cross-section, the torsional moment of inertia ${{I}_{T}}$ is equivalent to the polar Area moment of inertia ${{I}_{P}}$. The largest shear stresses $\tau $ are found at the edges of this component. The maximum Shear stress is calculated as follows: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ . The torsional Resistance moment ${{R}_{T}}$ represents the component's cross-sectional geometry.
-
Example sentences:
- It is necessary to ascertain the resistance moment to determine the maximum capacity of a component such as beam to withstandbending and torsional stresses.
- The anti-torsion elements are also to be removed as appropriate for this purpose.
- The anti-torsion features of the heavy-duty Hinge in the groove remain effective.
- Use a slotted screwdriver to break off the anti-torsion features.

torsional stress
Description:
It is necessary to ascertain the resistance moment to determine the maximum capacity of a component such as beam to withstandbending and torsional stresses.
-
Example sentences:
- It is necessary to ascertain the resistance moment to determine the maximum capacity of a component such as beam to withstandbending and torsional stresses.

esfuerzo de torsión

扭转
Description:
扭转是指以扭矩 MT形式作用于物体上并产生扭曲 $\vartheta $ 的受力与变形形式。扭矩的建立需要很多条件,如横向力和杠杆臂d。 形变量取决于被扭曲构件横截面的几何形状。例如,一个圆形横截面的组件,不产生任何翘曲。单位长度的扭曲 $\frac{d\vartheta }{dx}$ 可以根据以下物理量来计算:主动扭矩 ${{M}_{T}}$ ,材料特性相关的剪切模量 G,横截面的几何形状和扭转惯性矩 ${{I}_{T}}$ 。 下式为扭力计算公式: $\frac{d\vartheta }{dx}=\frac{{{M}_{T}}}{G\cdot {{I}_{T}}}$ 。 构件具有圆形截面时,扭转惯性矩 ${{I}_{T}}$ 等于 截面极惯性矩 ${{I}_{P}}$ 。 最大剪应力 $\tau $ 作用于构件边缘。且剪应力最大值的计算公式如下: ${{\tau }_{\max }}=\frac{{{M}_{T}}}{{{R}_{T}}}$ 。 扭转阻力矩 ${{R}_{T}}$ 反映了构件的横截面几何形状。 圆形截面体的扭转