statische Bestimmheit (Feminin)

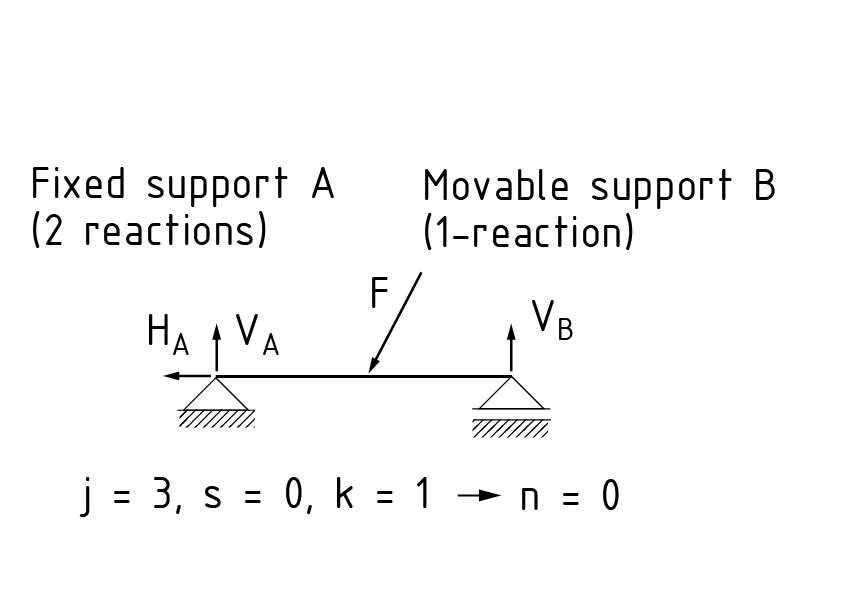
Description: A static system is said to exhibit static determinacy when it has the same number of degrees of freedom as support reactions. The support reactions can be calculated based on the conditions of Equilibrium of the external loads. There are six conditions of equilibrium in a three-dimensional space. The first three describe the sum total of all forces in all three dimensions (x, y, z). The other three equations describe the sum total of moments around the three spatial axes. All the equations result in zero. The degree n of static indeterminacy is calculated as follows: $n=j+s-6k$ (three-dimensional) and/or $n=j+s-3k$ (two-dimensional) j is the sum total of all the reactions from the supports (valency), s is the sum total of all the reactions from the connections (valency) and k is the number of bodies to be modelled in a free body diagram. If we consider a Truss with a number z of joints, s members and a supporting forces, the degree of indeterminacy is calculated thus: $n=a+s-2s$ If n = 0, the truss exhibits static determinacy.