Steiner'scher Verschiebesatz (Maskulin)

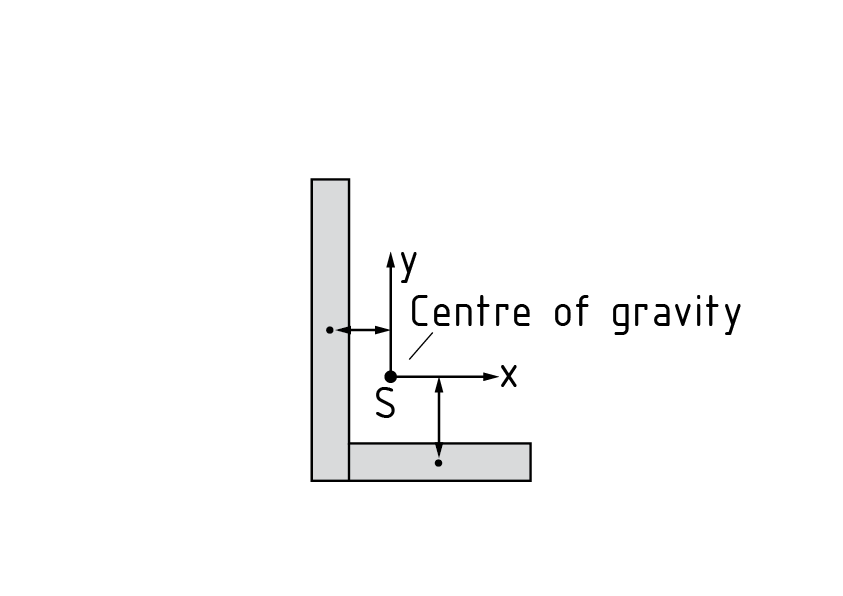
Description: The parallel-axis theorem (Steiner's theorem) is used to transform area moments of inertia onto an axis running parallel to the centroid (gravity) axis. In the case of components comprising composite cross-sectional areas, the parallel-axis theorem can be used to determine the area moments of the full cross-sections. The Area moment of inertia of a composite cross-section (see diagram with example of L section) is calculated as follows: Split the full cross-section into simple cross-sectional shapes (e.g. square, triangle, circle) Determine the individual centres of gravity Calculate the area moments of inertia (of the relevant cross-sections) or obtain these values from appropriate tables (${{I}_{y~}}$and ${{I}_{z~}}$) Transform the relevant area moments of inertia using the parallel-axis theorem: \[{{I}_{{\bar{y}}}}={{I}_{y}}+\bar{z}_{s}^{2}A\], ${{I}_{{\bar{z}}}}={{I}_{z}}+\bar{y}_{s}^{2}A$, \[{{I}_{\bar{y}\bar{z}}}={{I}_{yz}}-\bar{y}_{s}^{{}}\bar{z}_{s}^{{}}A\] $\bar{z}_{s}^{2}A$ and \[\bar{y}_{s}^{2}A\] are both called the Steiner's share. The relevant area A is multiplied by the square of the distance between the individual and common centres of gravity. Adding up the relevant transformed area moments of inertia to obtain a total area moment of inertia indicates the area moment of the full cross-section