Spannungstensor (陽性)

Beschreibung:

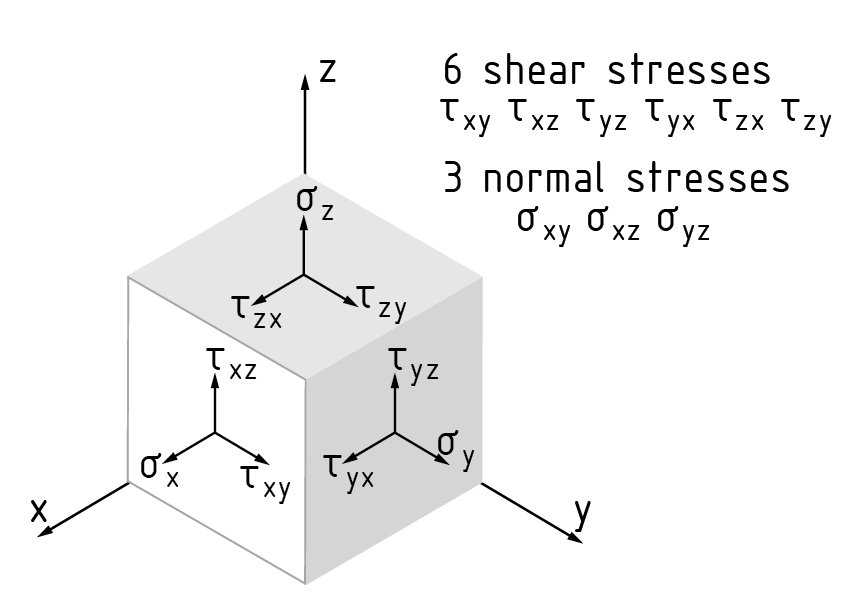
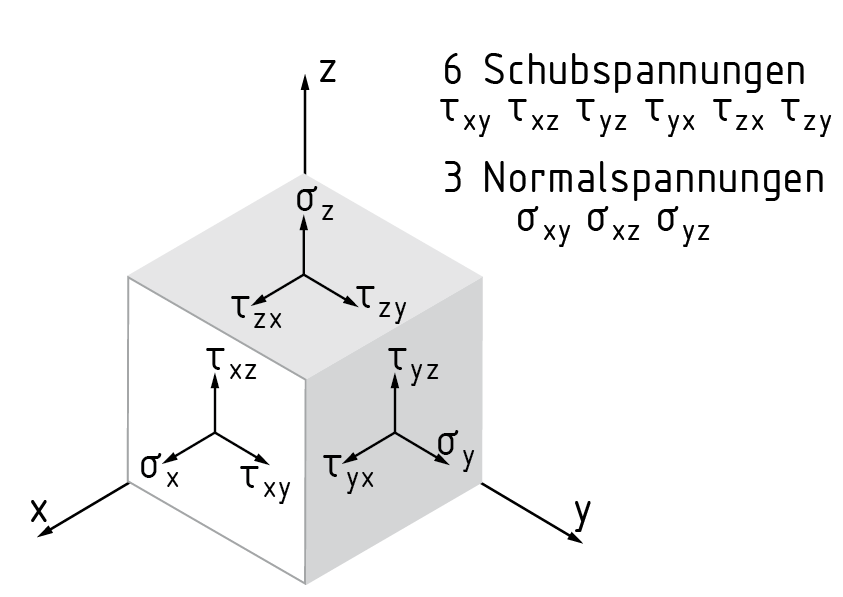
Ein Spannungstensor S beschreibt den Spannungszustand in einem Punkt eines Körpers. Sowohl die wirkenden Normal- als auch die Schubspannungen sind im Spannungstensor enthalten. Senkrecht auf den Schnittflächen eines freigeschnittenen Spannungswürfels stehen die drei Normalspannungen $({{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}})$. Sie sind durch wirkende Zug- oder Druckkräfte bedingt. Die zwei Schubkräfte jeder Schnittfläche liegen jeweils in einer Ebene und stehen senkrecht auf der Normalspannung.

Insgesamt werden sechs Schubspannungen unterschieden: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$. Schubspannungen werden z. B. durch Biegung oder Torsion eines Körpers erzeugt.

\[S=\left( \begin{matrix}{{\sigma }_{x}} & {{\tau }_{xy}} & {{\tau }_{xz}} \\{{\tau }_{yx}} & {{\sigma }_{y}} & {{\tau }_{yz}} \\{{\tau }_{zx}} & {{\tau }_{zy}} & {{\sigma }_{z}} \\\end{matrix} \right)\]

Die erste Stelle des Indexes des Schubspannungsvektors (z. B. z bei ${{\tau }_{zy}}$) gibt dessen Zugehörigkeit zu der Spannungsnormalen (hier: z-Achse) an, die zweite Stelle die Richtung des Schubspannungsvektors (hier: y-Achse).

Normal- und Schubspannungen am Spannungswürfel

Beispielsätze:

Ein SpannungstensorS beschreibt den Spannungszustand in einem Punkt eines Körpers.
Sowohl die wirkenden Normal- als auch die Schubspannungen sind im Spannungstensor enthalten.

stress tensor (中性)

Description: A stress tensor S indicates the stress state at a given point in a body. The stress tensor includes both the normal and shear stresses acting on the body. The three normal stresses $({{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}})$ act perpendicular to the sectional areas of an isolated stress cube. They are attributable to active tensile or compressive forces. In each case, the two shear forces of each sectional area lie in a given plane and act perpendicular to the normal stress. There are a total of six different shear stresses: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$. Shear stresses are generated, for example, through Bending or Torsion in a body. \[S=\left( \begin{matrix}{{\sigma }_{x}} & {{\tau }_{xy}} & {{\tau }_{xz}} \\{{\tau }_{yx}} & {{\sigma }_{y}} & {{\tau }_{yz}} \\{{\tau }_{zx}} & {{\tau }_{zy}} & {{\sigma }_{z}} \\\end{matrix} \right)\] The first index position in the Shear stress vector (e.g. z in ${{\tau }_{zy}}$) indicates to which stress normal the shear stress belongs (in this case the z-axis), while the second position indicates the direction of the shear stress vector (in this case the y-axis).

Normal and shear stresses on a stress cube

Example sentences:

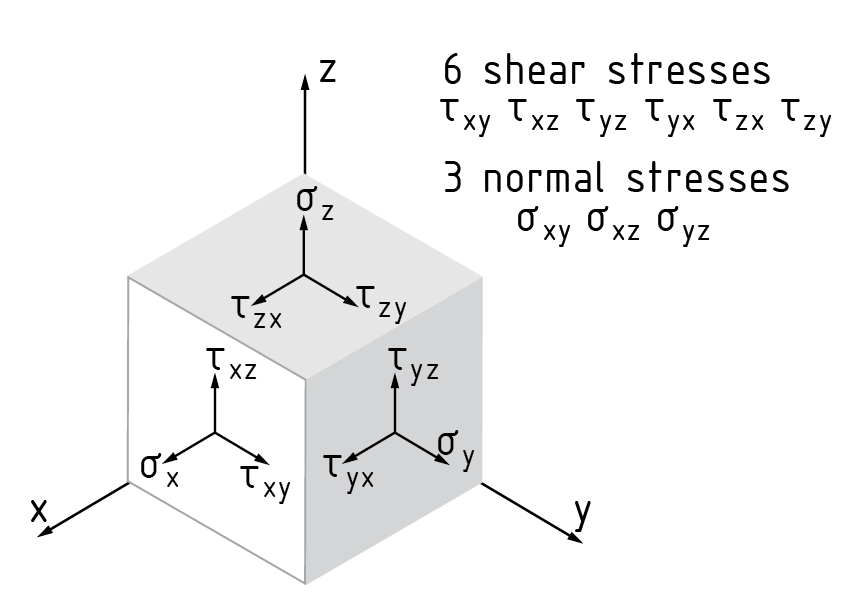
A stress tensorS indicates the stress state at a given point of a body.
The stress tensor includes both normal and shear stresses.

tensor de esfuerzo (中性)

Tensor de esfuerzos

Description:

Un tensor de esfuerzos S indica el estado de esfuerzo en un punto dado de un cuerpo. El tensor de esfuerzos incluye tanto el esfuerzo normal como el esfuerzo de corte que actúan en el cuerpo. Los tres esfuerzos normales $({{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}})$ actúan perpendiculares a las áreas de sección de un cubo de esfuerzo aislado. Son atribuibles a las fuerzas de tensión o compresión activas. En cada caso, las dos fuerzas de corte de cada área de sección caen en un plano dado y actúan perpendiculares al esfuerzo normal.

Hay un total de seis esfuerzos de corte diferentes: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$ . Los esfuerzos de corte se generan, por ejemplo, al flexionar o torcer un cuerpo.

$S=\left( \begin{matrix} {{\sigma }_{x}} & {{\tau }_{xy}} & {{\tau }_{xz}} \\ {{\tau }_{yx}} & {{\sigma }_{y}} & {{\tau }_{yz}} \\ {{\tau }_{zx}} & {{\tau }_{zy}} & {{\sigma }_{z}} \\\end{matrix} \right)$

La primera posición de índice en el vector de esfuerzo de corte (por ejemplo, z en ${{\tau }_{zy}}$ ) indica a qué normal de esfuerzo pertenece el esfuerzo por corte (en este caso el eje z), mientras que la segunda posición indica la dirección del vector de esfuerzo de corte (en este caso el eje y).

Esfuerzos normal y de corte en un cubo de esfuerzos

Tensor de esfuerzos

Description:

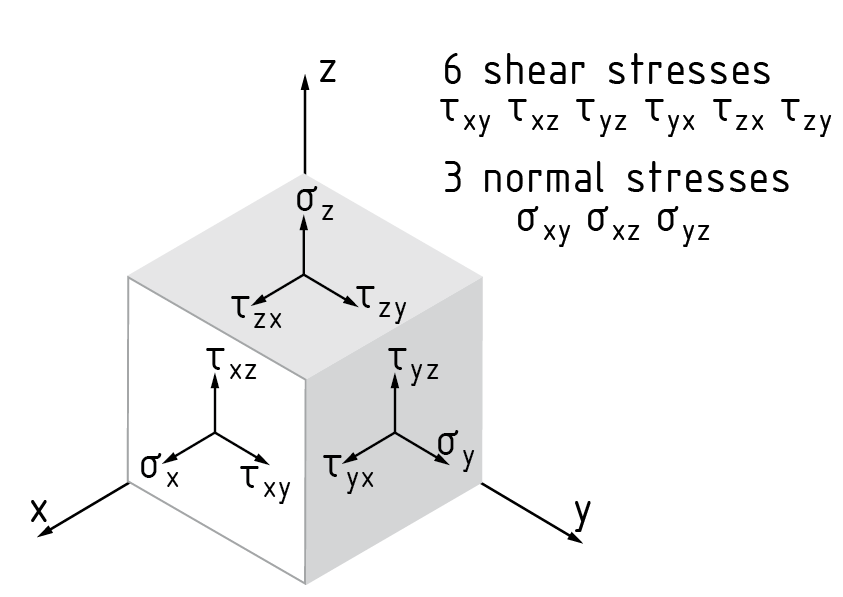
Un tensor de esfuerzos S indica el estado de esfuerzo en un punto dado de un cuerpo. El tensor de esfuerzos incluye tanto el esfuerzo normal como el esfuerzo de corte que actúan en el cuerpo. Los tres esfuerzos normales $({{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}})$ actúan perpendiculares a las áreas de sección de un cubo de esfuerzo aislado. Son atribuibles a las fuerzas de tensión o compresión activas. En cada caso, las dos fuerzas de corte de cada área de sección caen en un plano dado y actúan perpendiculares al esfuerzo normal.

Hay un total de seis esfuerzos de corte diferentes: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$ . Los esfuerzos de corte se generan, por ejemplo, al flexionar o torcer un cuerpo.

$S=\left( \begin{matrix} {{\sigma }_{x}} & {{\tau }_{xy}} & {{\tau }_{xz}} \\ {{\tau }_{yx}} & {{\sigma }_{y}} & {{\tau }_{yz}} \\ {{\tau }_{zx}} & {{\tau }_{zy}} & {{\sigma }_{z}} \\\end{matrix} \right)$

La primera posición de índice en el vector de esfuerzo de corte (por ejemplo, z en ${{\tau }_{zy}}$ ) indica a qué normal de esfuerzo pertenece el esfuerzo por corte (en este caso el eje z), mientras que la segunda posición indica la dirección del vector de esfuerzo de corte (en este caso el eje y).

Esfuerzos normal y de corte en un cubo de esfuerzos

应力张量 (中性)

Description: 应力张量 S 表示一个物体内任意给定点的应力状态。应力张量是作用于物体上的正应力和剪应力的合作用力。三个正应力 $({{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}})$ 分别垂直作用于单元体彼此正交的三个截面，使截面间产生拉伸应力或压缩应力。在任何情况下，作用于任一给定截面上两个剪应力与此截面相切并与此截面的正应力彼此正交。总共产生 6 个不同的剪应力: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$ 。剪应力可由物体受到弯曲或扭转而产生。 $S=\left( \begin{matrix} {{\sigma }_{x}} & {{\tau }_{xy}} & {{\tau }_{xz}} \\ {{\tau }_{yx}} & {{\sigma }_{y}} & {{\tau }_{yz}} \\ {{\tau }_{zx}} & {{\tau }_{zy}} & {{\sigma }_{z}} \\\end{matrix} \right)$ 剪应力矢量的第一个角标字母 (如 ${{\tau }_{zy}}$ 中的 z) 指的是垂直于剪应力的应力方向（即此处的z轴）, 第二个角标字母指的是该剪应力矢量的方向（即此处的y轴）。单元体上的正应力和剪应力