Goldener Schnitt (陽性)

Beschreibung:

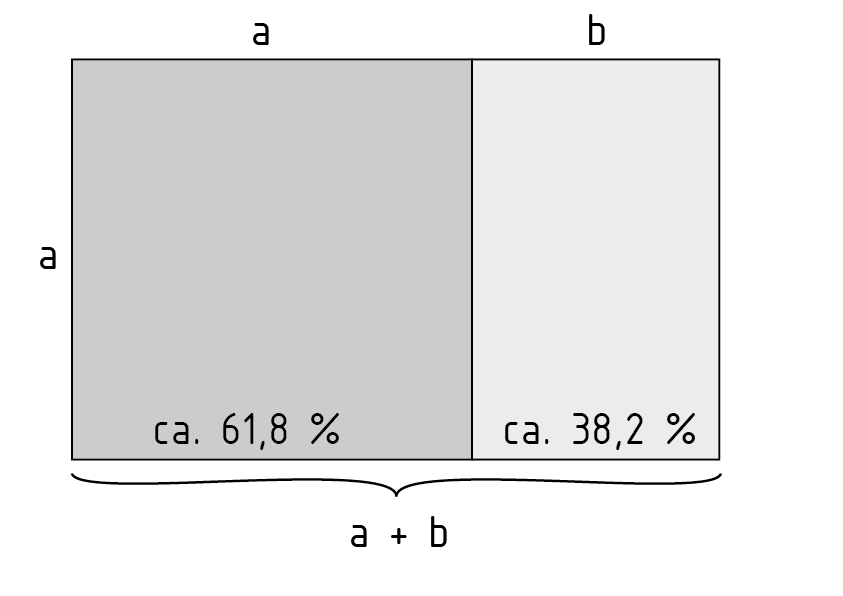
Der Goldene Schnitt ist ein bestimmtes Verhältnis, das die Gesamtlänge einer Strecke in Bezug auf die Länge der beiden Teilstrecken beschreibt. Ist der Quotient aus der Gesamtlänge und der größeren Teilstrecke a (Major) gleich dem Quotienten aus der größeren und kleineren Teilstrecke b (Minor), so liegt der Goldene Schnitt vor. Der Quotient aus a und b wird als Goldene Zahl $\phi $ bezeichnet$\phi =\frac{a}{b}=\frac{a+b}{a}$.

Ein Rechteck bzw. gleichschenkliges Dreieck mit dem Seitenverhältnis des Goldenen Schnittes wird Goldenes Rechteck bzw. Goldenes Dreieck genannt. Wird ein Kreis in zwei Winkel aufgeteilt und der Quotient aus dem größeren und kleineren Teil des Kreises entspricht der Goldenen Zahl, so handelt es sich bei dem größeren Winkel um den Goldenen Winkel $\psi $.

Mit Zeichenwerkzeug wie Lineal und Zirkel ist der Goldene Schnitt grafisch konstruierbar. Dabei ist zwischen der inneren und äußeren Teilung zu unterscheiden.

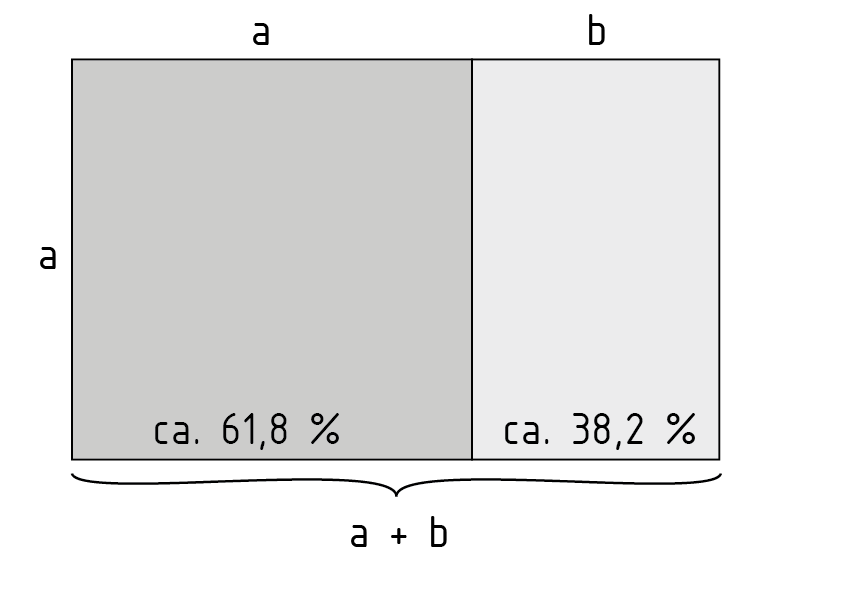
golden ratio (中性)

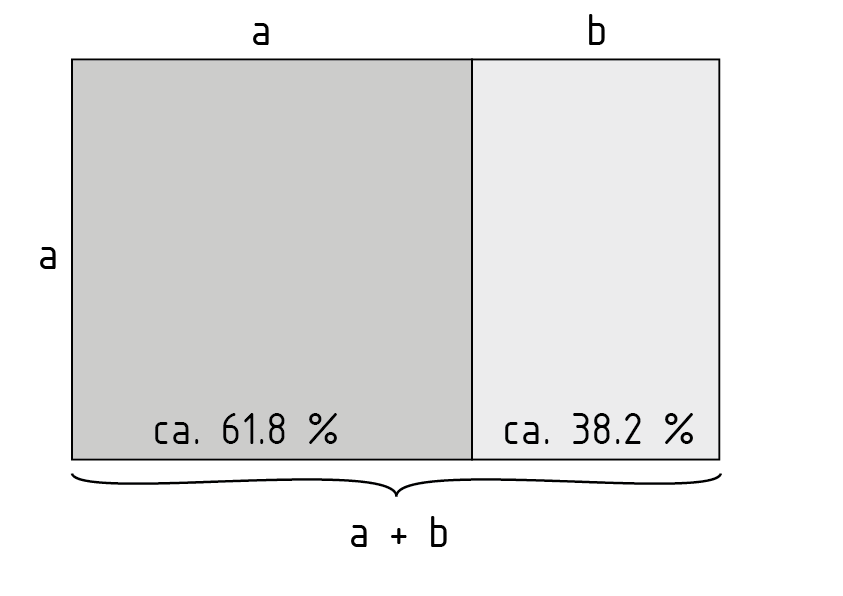
Description: The golden ratio is a specific ratio that defines the total length of a line segment in relation to the length of its two parts. If the quotient of the total length and the longer part a (major) equals the quotient of the longer part and the shorter part b (minor), the golden ratio applies. The quotient of a and b is referred to as the golden number $\phi $ where $\phi =\frac{a}{b}=\frac{a+b}{a}$. A rectangle / isosceles triangle whose sides are in the golden ratio is called a golden rectangle / golden triangle. If two angles are created by sectioning the circumference of a circle and the quotient of the larger and the smaller part of the circle is equivalent to the golden number, the larger angle is the golden angle $\psi $. The golden ratio can be created graphically using drawing instruments such as a ruler and compass. A distinction is made between the inner and outer sections.

proporción áurea (中性)

Description: La proporción áurea es una proporción específica que define la longitud total de un segmento de línea en relación con la longitud de sus dos partes. Si el cociente de la longitud total y la parte larga a (mayor) es igual al cociente de la parte más larga y la parte más corta b (menor), la proporción áurea aplica. El cociente de a y b es referido como número áureo $\phi $ donde $\phi =\frac{a}{b}=\frac{a+b}{a}$ . Un triángulo rectángulo/isósceles cuyos lados están dentro de la proporción áurea se llama rectángulo áureo/triángulo áureo. Si se crean dos ángulos dividiendo la circunferencia de un círculo y el cociente de la parte más grande y más pequeña del círculo es equivalente al número áureo, el ángulo mayor es el ángulo áureo $\psi $ . La proporción áurea puede crearse gráficamente usando instrumentos de dibujo como una regla y un compás. Se distingue entre las secciones internas y externas. Proporción áurea

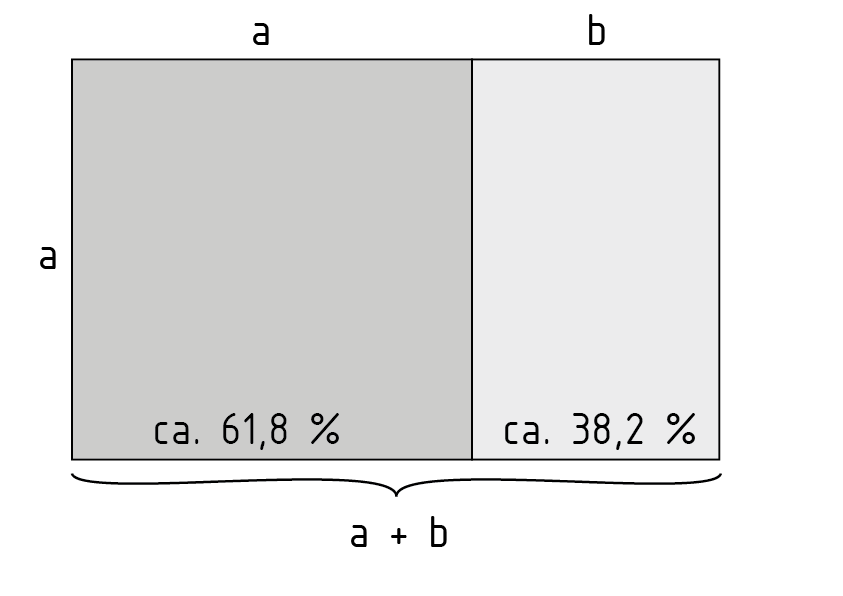
黄金比例 (中性)

Description: 黄金比例是一个特殊比例，它描述的是整条线段的长度与其分割后所形成两部分的长度之间的关系。如果整段长度与较长部分a（主要部分）的比值等于较长部分与较短部分b（次要部分）的比值, 那么该比值即为黄金比例。a与b的比值即为黄金分割数 $\phi $。其中 $\phi =\frac{a}{b}=\frac{a+b}{a}$。一个边长比例为黄金比例的矩形或者等腰三角形被称为黄金矩形/黄金三角形。如果两个角是通过圆周分割而成，并且圆的较大部分与较小部分的比例等于黄金分割比例，那么这个大角叫做黄金角 $\psi $。黄金比例以用图形表示，通过绘图工具如尺子和圆规画出，从而体现图形内部和外部之间的差异。黄金比例近义词黄金三角形黄金矩形黄金角