
一种定义
四种语言
0,1,2
- 德國
- 英語
- 中國
- 西班牙語
电感
电感是由于磁力线密度变化而产生电场的现象。磁力线密度的变化会在导体上产生磁场作用力。该原理的实际应用就是电动机,而如果作用力产生了电场的移动,那就是发电机。
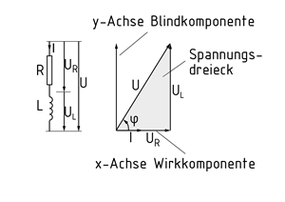
电流的变化能够改变电磁场,而电感的作用就是对电流的流动产生一个反方向的电磁力。纯电感会造成电流落后电压90°的相差。而实际电路中存在的电阻或者容抗则会产生可变的相差角 $\varphi$ .
在交流电路中,电感会产生感抗,这时,如果不考虑相差角,阻抗就是频率角度值 $\omega $ 和感抗的积。如果再考虑相差角度,这时候就可以计算出复数阻抗 $j\omega L $ 了。
等效示意图和矢量图
Induktivität
Eine Induktivität beschreibt das Entstehen eines elektrischen Feldes aufgrund der Änderung der magnetischen Flussdichte. Durch die Änderung der Flussdichte wird eine Kraft erzeugt, die auf den Leiter wirkt. Dieses Prinzip ist vom Motor und - wenn durch eine Kraft eine Bewegung im elektrischen Feld erfolgt - vom Generator bekannt.
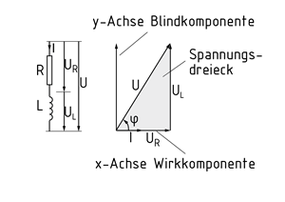
Bei einer Änderung des elektrischen Stromes ändert sich das magnetische Feld und die Induktivität induziert eine Gegenspannung. Diese induzierte Gegenspannung wirkt dem Stromfluss entgegen. Bei einer reinen Induktivität entsteht eine Phasenverschiebung, bei der der Strom der Spannung um 90° nacheilt. Durch ohmsche Widerstände oder Kapazitäten in realen Schaltungen ergibt sich ein variabler Phasenverschiebungswinkel$\varphi $.
Im Wechselstromkreis ruft eine Induktivität einen induktiven Blindwiderstand hervor, der sich ohne Betrachtung des Phasenverschiebungswinkels aus dem Produkt von der Kreisfrequenz ? und der Induktivität ergibt. Betrachtet man den Phasenwinkel, so ergibt sich die komplexe Impedanz$j\omega L$.
Inductancia
La inductancia es la creación de un campo eléctrico debido a un cambio en la densidad del flujo magnético. Este cambio en la densidad del flujo genera una fuerza que actúa en el conductor. Este principio se aplica a motores y, si la fuerza resulta en un movimiento en el campo eléctrico, a generadores.
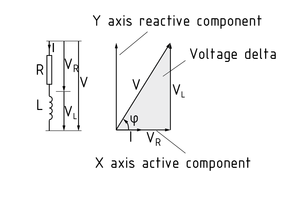
Un cambio en la corriente eléctrica altera el campo magnético y la inductancia induce una contra fuerza electromotriz que actúa contra el flujo de corriente. Una inductancia pura resulta en un cambio de fase donde la corriente desfasa el voltaje en 90°. Las resistencias óhmicas o capacitancias en circuitos reales producen un ángulo de cambio de fase $\varphi $ .
En un circuito de CA, una inductancia produce una reactancia inductiva que, si se ignora el ángulo de cambio de fase, es el producto de la frecuencia angular $\omega $ y la inductancia. Tomando en consideración el ángulo de fase, este proporciona la impedancia compleja $j\omega L $ .
Diagrama equivalente y diagrama vector
