
一种定义
四种语言
0,1,2
- 德國
- 英語
- 中國
- 西班牙語
微分学
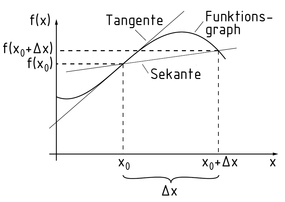
微分学是数学分析领域的一个分支,主要研究函数图像的变化过程。微分可以计算函数 $f(x)$ 在任意点P处的切线斜率。导数就是在无穷小的区间内计算斜率的变化。
连接函数图像上任意两点的直线,称为这条曲线的割线。这两个点的横坐标的增量记作 $\Delta x$,在其趋于无穷小时,计算得到函数的导数。
求导时为避免不必要的重复运算,对于一些典型函数导数可以参照导数对照表。对于表中没有的函数进行求导时,要遵循以下求导法则:
积分与微分互为逆运算。函数 $f(x)$ 的原函数 $F(x)$ 的导数仍是 $f(x)$,即 $F'(x)=f(x)$。
函数图像的切线和割线
近义词
微分法
求导
求导法则
Differenzialrechnung
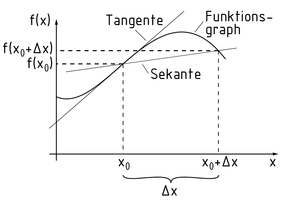
Die Differentialrechnung als Teilgebiet der Analysis beschäftigt sich mit dem Verlauf von Funktionsgraphen. Mit der Differenzialrechnung ist in jedem Punkt P einer Funktion $f(x)$ die Steigung der Tangente durch diesen Punkt berechenbar. In einem infinitesimal kleinen Intervall ist dabei die Änderung der Steigung zu berechnen. Dies wird als Ableiten bezeichnet.
Eine Gerade, die durch zwei Punkte auf einem Funktionsgraphen verläuft, heißt Sekante. Der Abstand der beiden Punkte in x Richtung ist $\Delta x$. Bei der sogenannten h-Methode wird der Differenzialquotient bestimmt und die Breite von $\Delta x$als infinitesimal klein angenommen.
Typische Ableitungen sind in Tabellenwerken zusammengefasst und müssen somit nicht jedes Mal neu berechnet werden. Sind die abzuleitenden Funktionen nicht im Tabellenwerk enthalten, kann auf folgende Ableitungsregeln zurückgegriffen:
- Konstante Funktion
- Faktorregel
- Summenregel
- Produktregel
- Quotientenregel
- Reziprokenregel
- Potenzregel
- Kettenregel
- Umkehrregel
- Logarithmische Ableitung
- Leibnizsche Regel
- Formel von Faà di Bruno
Die Differenzialrechnung ist die Umkehrung der Integralrechnung. Das Ableiten einer Stammfunktion $F(x)$ von einer Funktion liefert die Funktion $f(x)$ selbst. Es gilt: $F'(x)=f(x)$.
Differential calculus
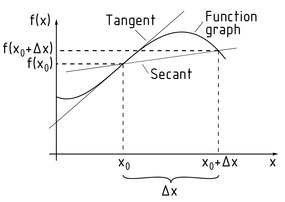
Differential calculus is a branch of analysis that deals with the path of function graphs. Differential calculus makes it possible to calculate the gradient of the tangent through every point P of a function $f(x)$. The change in the gradient is then calculated at infinitesimally small intervals. This is referred to as derivation.
A straight line that passes through two points on a function graph is called a secant. The distance between the two points in the x direction is $\Delta x$. The h-method is used to determine the differential quotient and the width of $\Delta x$is assumed to be infinitesimally small.
Reference tables list typical derivatives so as to avoid having to re-calculate them from scratch every time. If the functions to be derived are not included in such tables, the following rules of derivation can be used:
- Constant function
- Constant factor rule
- Sum rule
- Product rule
- Quotient rule
- Reciprocal rule
- Power rule
- Chain rule
- Inverse rule
- Logarithmic derivative
- Leibnitz's rule
- Faà di Bruno's formula
Differential calculus is the opposite of Integral calculus. Deriving an antiderivative $F(x)$ from a function gives the function $f(x)$ itself. The formula $F'(x)=f(x)$ applies.
Cálculo diferencial
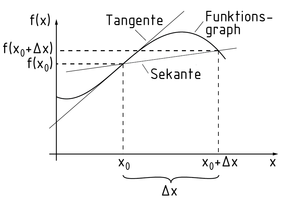
El cálculo diferencial es una rama del análisis que trata con el paso de las gráficas de función. El cálculo diferencial hace posible el cálculo del gradiente de la tangente a través de cada punto P de una función $f(x)$ . El cambio en el gradiente luego se calcula en pequeños intervalos infinitesimales. Esto es referido como derivación.
Una línea recta que pasa a través de dos puntos en una gráfica de función se llama secante. La distancia entre los dos puntos en dirección x es $\Delta x$ . El método h se usa para determinar el cociente diferencial y el ancho de $\Delta x$ se asume como infinitesimalmente pequeño.
Las tablas de referencia enumeran las derivadas típicas para evitar tener que recalcularlas desde el principio cada vez. Si las funciones a ser derivadas no se incluyen en dichas tablas, se pueden usar las siguientes reglas de derivación:
El cálculo diferencial es el opuesto al cálculo integral. Derivar un antiderivada $F(x)$ de una función da como resultado la función $f(x)$ en sí. Aplica la fórmula $F'(x)=f(x)$ .
Tangente y secante de una gráfica de función
