微分元件

Sprungantwort D-Glied

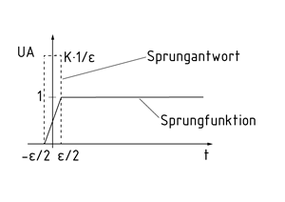
在闭环控制系统中，微分元件是专门与其他的控制元件结合使用的传递元件。微分元件的输出变量不对控制误差的大小做出反应，而是对输入变量的速度做出反应，从而对控制误差的变化速度作出响应。

如果输入信号以恒定的速度发生改变，那么微分元件的输出信号也将因此保持为常数。如果输入发生突然增加，输出将出现激增。技术系统适用以下简化原则：阶跃函数不是骤升而是一个持续的，非常陡峭的过渡过程。如果条件与函数不同，那么输出将出现一个非常高而窄的尖峰$K_D$ . 输出信号的振幅取决于阶跃函数的斜率范围 $-\varepsilon /2$ to $\varepsilon /2$ 。其中斜率为 $\frac{\Delta {{x}_{e}}}{\Delta t}=\frac{1}{\varepsilon }$ ，而微分作用系数为 ${{K}_{D}}=\frac{{{U}_{A}}\cdot \Delta t}{\Delta e}=\frac{{{U}_{A}}\cdot \varepsilon }{1}$.

微分元件的阶跃响应

近义词

微分元件

D-Glied

Sprungantwort D-Glied

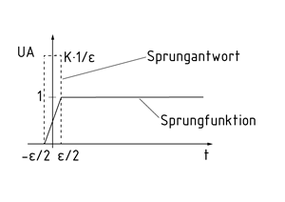
Das D-Glied ist ein Übertragungsglied in der Regelungstechnik, das ausschließlich in Verbindung mit anderen Regelgliedern eingesetzt wird. Die Ausgangsgröße des D-Gliedes reagiert nicht auf die Höhe der Regelabweichung, sondern auf die Änderungsgeschwindigkeit der Eingangsgröße und damit der Regelabweichung.

Bei einer konstanten Änderungsgeschwindigkeit des Eingangssignals ist das Ausgangssignal des D-Gliedes ebenfalls konstant. Ein sprungförmiger Anstieg am Eingang ruft am Ausgang einen Nadelimpuls hervor. Für technische Systeme gilt die Vereinfachung, dass die Sprungfunktion keinen Sprung, sondern einen kontinuierlichen, sehr steilen Übergang aufweist. Die Differenzierung dieser Funktion liefert einen sehr hohen und schmalen Impuls mit K_D. Die Größe des Ausgangssignals ist dabei abhängig von der Steigung der Sprungfunktion im Bereich von $-\varepsilon /2$ bis $\varepsilon /2$. Die Steigung beträgt $\frac{\Delta {{x}_{e}}}{\Delta t}=\frac{1}{\varepsilon }$und der Differenzierbeiwert ${{K}_{D}}=\frac{{{U}_{A}}\cdot \Delta t}{\Delta e}=\frac{{{U}_{A}}\cdot \varepsilon }{1}$.

D element

Step response of D element

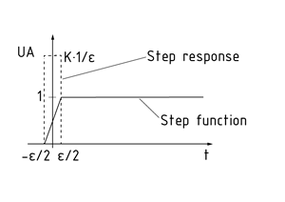
A D element is a transfer element in a Closed-loop control system that is used exclusively in combination with other control elements. The D element's output variable does not respond to the magnitude of the control error but to the speed at which the input variable and thus the control error change.

If the input signal changes at a constant speed, the D element's output signal is also constant. A sudden increase at the input causes a spike at the output. The following simplification applies to technical systems: The step function is not a sudden jump but a continuous, very steep transition. Differentiating this function produces a very tall, narrow spike with K_D. The amplitude of the output signal depends on the slope of the step function in the range $-\varepsilon /2$ to $\varepsilon /2$. The slope is $\frac{\Delta {{x}_{e}}}{\Delta t}=\frac{1}{\varepsilon }$and the derivative-action coefficient ${{K}_{D}}=\frac{{{U}_{A}}\cdot \Delta t}{\Delta e}=\frac{{{U}_{A}}\cdot \varepsilon }{1}$.

Elemento D

Respuesta de paso del elemento D

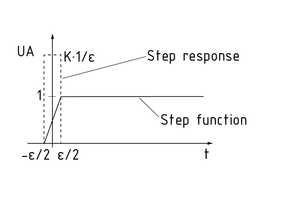
Un elemento D es un elemento de transferencia de un sistema de control de bucle cerrado que se usa exclusivamente en combinación con otros elementos de control. La variable de salida del elemento D no responde a la magnitud del error de control, sino a la velocidad en la que cambia la variable de entrada y por lo tanto el error de control.

Si la señal de entrada cambia a una velocidad constante, la señal de salida del elemento D también es constante. Un incremento repentino en la entrada genera un pico en la salida. La siguiente simplificación aplica a los sistemas técnicos: La función de paso no es un salto repentino sino una transición continua muy pronunciada. Diferenciar esta función produce un pico muy alto y estrecho con $K_D$. La amplitud de la señal de salida depende de la pendiente de la función de paso en el rango $-\varepsilon /2$ a $\varepsilon /2$. La pendiente es $\frac{\Delta {{x}_{e}}}{\Delta t}=\frac{1}{\varepsilon }$ y el coeficiente de acción derivada ${{K}_{D}}=\frac{{{U}_{A}}\cdot \Delta t}{\Delta e}=\frac{{{U}_{A}}\cdot \varepsilon }{1}$.

Respuesta de paso del elemento D