
一种定义
四种语言
0,1,2
- 德國
- 英語
- 中國
- 西班牙語
动强度

构件的动强度是指可变载荷下构件产生的变形抗力。疲劳试验可用来确定最大应力循环数 N,其试验数据可以通过沃勒曲线直观的显示。
应力循环数表明了材料在名义应力幅值 ${{S}_{a}}$ 下承受的载荷交变次数。如果材料破裂失效,则表明已经达到了最大的应力循环数。
沃勒曲线( s—N 曲线)可分为三部分。
第一部分是指接近 ${{10}^{4}}$ 次内的应力循环,被称为低周疲劳LCF。此时构件的动强度几乎等于静拉伸强度。
第二部分是高周疲劳 HCF ,指接近 ${{10}^{4}}$ 到 $2\cdot {{10}^{6}}$ 次之间的应力循环,这一段的曲线路径相当于沃勒直线,是沃勒曲线中的一段线性变化过程。
最后一部分是指疲劳强度(例如铝的应力循环数极限为 $>{{10}^{6}}$ 或 $>{{10}^{7}}$ ),构件因为过载而失效。
沃勒曲线分为三部分
Schwingfestigkeit

Die Schwingfestigkeit beschreibt den Widerstand eines Bauteils gegenüber der Verformung bei veränderlicher Belastung. Aus Dauerschwingversuchen werden die maximalen Schwingspielzahlen N ermittelt und in Form einer Wöhlerkurve grafisch dargestellt.
Die Schwingspielzahlen beschreiben die Anzahl an Lastwechseln, die ein Werkstoff unter den Nennspannungsamplituden ${{S}_{a}}$ erfährt. Kommt es zum Versagen des Bauteils, also zum Bruch, ist die maximale Schwingspielzahl erreicht.
Es werden drei Bereiche in der Wöhlerkurve unterschieden.
- Der erste Bereich befindet sich unterhalb von ca. \[{{10}^{4}}\] Schwingspielen und wird als Kurzzeitschwingfestigkeit K bezeichnet. Diese Schwingfestigkeit ist etwa mit der statischen Festigkeit eines Bauteils vergleichbar.
- Im folgenden Abschnitt, dem Bereich der Zeitschwingfestigkeit Z oder auch Zeitfestigkeit (ca. \[{{10}^{4}}\] bis \[2\cdot {{10}^{6}}\]), entspricht der Kurvenverlauf der sogenannten Wöhlerlinie. Die Wöhlerlinie beschreibt den linear verlaufenden Teil der Wöhlerkurve.
- Im Bereich der Dauerfestigkeit D (Schwingspiele $>{{10}^{6}}$ bzw. $>{{10}^{7}}$, u. a. bei Aluminium) tritt das Versagen des Bauteils aufgrund hoher Belastungen ein.
Dynamic strength
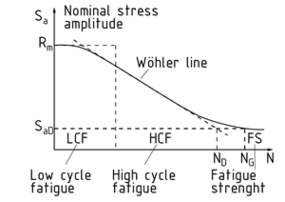
A component's dynamic Strength is its Resistance to deformation when subjected to a variable load. Fatigue tests are used to determine the maximum numbers of stress cycles N and this data is displayed graphically in the form of a Wöhler curve.
The numbers of stress cycles indicate how many alternations of load a Material is subjected to under the nominal stress amplitudes ${{S}_{a}}$. If the component fails, i.e. ruptures, the maximum number of stress cycles has been reached.
The Wöhler (stress-number) curve is split into three sections.
- The first is the range below approx. \[{{10}^{4}}\] stress cycles and is referred to as low-cycle fatigue LCF. This dynamic strength is roughly equivalent to a component's static tensile strength.
- In the following section, high cycle fatigue HCF (approx. \[{{10}^{4}}\] to \[2\cdot {{10}^{6}}\]), the path of the curve corresponds to the Wöhler line. This is the linear part of the Wöhler curve.
- In the final section, fatigue strength ($>{{10}^{6}}$ or $>{{10}^{7}}$ stress cycles, for e.g. aluminium), the component fails due to high loads.
Resistencia dinámica
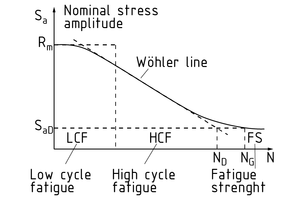
La resistencia dinámica de un componente es su resistencia a la deformación cuando está sujeto a una carga variable. Las pruebas de fatiga se usan para determinar el número de ciclos de esfuerzo N máximo y estos datos se muestran gráficamente en forma de una curva de Wöhler.
El número de ciclos de esfuerzo indica a cuántas alternaciones de carga está sujeto un material bajo las amplitudes de esfuerzo nominal ${{S}_{a}}$ . Si el componente falla, es decir, se rompe, se habrá alcanzado el número máximo de ciclos de esfuerzo.
La curva de Wöhler (número-esfuerzo) se divide en tres secciones.
La primera es el rango debajo de aproximadamente ${{10}^{4}}$ ciclos de esfuerzo y es referida como fatiga de ciclos bajos FCB. Esta resistencia dinámica es apenas equivalente a una resistencia a la tensión estática del componente.
En la siguiente sección, la fatiga de ciclos altos FCA (aprox. ${{10}^{4}}$ a $2\cdot {{10}^{6}}$ ), la ruta de la curva corresponde a la línea de Wöhler. Esta es la parte lineal de la curva de Wöhler.
En la sección final, la resistencia a la fatiga ( $>{{10}^{6}}$ o $>{{10}^{7}}$ ciclos de esfuerzo, para, por ejemplo, el aluminio), el componente falla debido a las altas cargas.
Curva de Wöhler mostrando las tres secciones
