抛物轨迹

Wurfbahn ohne Luftwiderstand

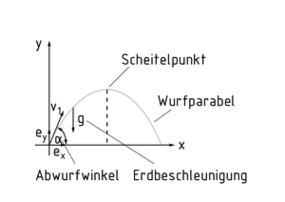
抛物轨迹是指当一个物体被抛出时所遵循的路径，可在坐标系中表示。典型情况是横向x 轴代表物体运动的距离（沿x方向），纵向y轴代表抛的高度（沿y方向）。

在斜抛情况下，当忽略空气阻力时，物体的运动轨迹呈抛物线状.。在坐标系的原点处，被抛物体具有初始速度 ${{v}_{1}}$和角度$\alpha $。重力加速度 $g=9.81\frac{m}{{{s}^{2}}}$ 会带动抛物曲线同时使物体速度减小。当物体到达曲线顶点时，速度的水平分量为0，同时具有最大的势能。在接下来的运动轨迹中，物体的势能逐渐转化成动能。在自由落体时，由于受到重力加速度g的影响，物体在落地前速度不断增加。

忽略空气阻力的抛物轨迹

Wurfbahn

Wurfbahn ohne Luftwiderstand

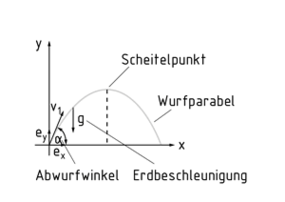
Die Wurfbahn beschreibt die Bahnkurve eines geworfenen Körpers. Sie lässt sich in einem Koordinatensystem auftragen. Typischerweise wird die horizontale Achse x dabei als Entfernung (x-Richtung) und die vertikale Achse y als Höhe (y-Richtung) des Wurfes bezeichnet.

Unter Vernachlässigung des Luftwiderstandes ist die Bahnkurve eines Körpers im Falle des schiefen Wurfes parabelförmig. Im Ursprung des Koordinatensystems hat der geworfene Körper die Geschwindigkeit ${{v}_{1}}$ mit dem Winkel $\alpha $. Die Erdbeschleunigung g mit $g=9,81\frac{m}{{{s}^{2}}}$ ist für ein Abflachen der Kurve und für die Verminderung der Geschwindigkeit des geworfenen Körpers verantwortlich. Im Scheitelpunkt der Kurve hat die vertikale Geschwindigkeitskomponente den Wert Null. Hier besitzt der Wurfkörper die maximale potentielle Energie. Im folgenden Abschnitt der Wurfbahn wandelt sich diese wieder in Kinetische Energie um. Wie bei einem freien Fall nimmt die Geschwindigkeit des Körpers durch die Wirkung der Erdbeschleunigung g wieder zu, bis er schließlich den Boden erreicht.

Trajectory of a projectile

Trajectory of a projectile without air resistance

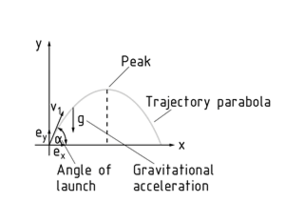
The trajectory of a projectile is the path that a body follows when it has been thrown. It can be depicted in a coordinate system. Typically, the horizontal x axis stands for the distance that the object travels (in direction x) and the vertical y axis stands for the height (in direction y) of the throw.

In the case of an oblique throw and when disregarding air Resistance, the trajectory of a body takes the shape of a parabola. At the origin of the coordinate system, the thrown body has Velocity ${{v}_{1}}$ and angle $\alpha $. Gravitational acceleration g at $g=9.81\frac{m}{{{s}^{2}}}$ is responsible for levelling the curve and reducing the velocity of the thrown body. At the peak of the curve, the vertical component of velocity is zero. This is where the thrown body has maximum potential energy. In the following section of the trajectory, this is converted back into Kinetic energy. As in the case of free fall, the velocity of the body begins to increase again due to the effect of gravitational acceleration g, until it finally reaches the ground.

Trayectoria de un proyectil

Trayectoria de un proyectil sin resistencia del aire

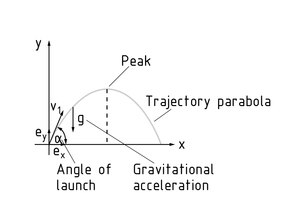
La trayectoria de un proyectil es la ruta que un cuerpo sigue cuando ha sido lanzado. Puede ser representada en un sistema coordinado. Típicamente, el eje horizontal x representa la distancia que el objeto viaja (en dirección x) y el eje vertical y representa la altura (en dirección y) del tiro.

En el caso de un tiro oblicuo y cuando se desestime la resistencia del aire, la trayectoria de un cuerpo toma la forma de una parábola. En el origen del sistema coordinado, el cuerpo lanzado cuenta con una velocidad ${{v}_{1}}$ y un ángulo $\alpha $. La aceleración gravitacional g en $g=9.81\frac{m}{{{s}^{2}}}$ es responsable de nivelar la curva y reducir la velocidad del cuerpo lanzado. En el pico de la curva, el componente vertical de velocidad es cero. Aquí es donde el cuerpo lanzado tiene la energía potencial máxima. En la siguiente sección de la trayectoria, esto se convierte nuevamente en energía cinética. Al igual que en el caso de la caída libre, la velocidad del cuerpo comienza a incrementarse nuevamente debido al efecto de la aceleración gravitacional g, hasta que finalmente llega al suelo.

Trayectoria de un proyectil sin resistencia del aire