
一种定义
四种语言
0,1,2
- 德國
- 英語
- 中國
- 西班牙語
平面应力状态
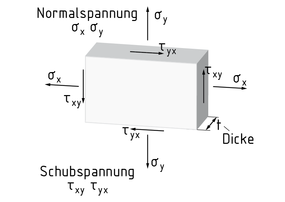
平面应力状态是指所取单元体厚度为无穷小量 t,即可将应力分量视为处于同一坐标平面内。这时只存在两个不同的正应力 ${{\sigma }_{x}},{{\sigma }_{y}}$ 和剪应力 ${{\tau }_{xy}}={{\tau }_{yx}}$ 。这种情况下,正应力和剪应力都均匀作用于整个平面单元上。
平面应力状态
如果平面单元与轴线存在一定角度(既不平行也不垂直) $\varphi $ ,必须应用变换方程将应力分量 ( ${{\sigma }_{x}},{{\sigma }_{y}}$ 和 ${{\tau }_{xy}}$ ) 根据相交角 $\varphi $ 进行分解(变为 ${{\sigma }_{\xi }},{{\sigma }_{\eta }}$ 和 ${{\tau }_{\zeta \eta }}$ )。
最大应力分量以一定角度相交于平面单元。作用于这个平面的正应力被称为主应力 ${{\sigma }_{1}}$ 和 ${{\sigma }_{2}}$ 。它们相互垂直并形成主坐标系。 假设第一主应力 ${{\sigma }_{1}}$ 的值大于第二主应力 ${{\sigma }_{2}}$ 。
Ebener Spannungszustand
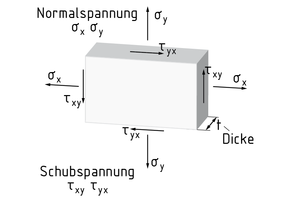
Der ebene Spannungszustand herrscht in Scheiben mit sehr geringer Dicke t. Es kann somit angenommen werden, dass zweidimensionale wirkenden Spannungen vorliegen Es sind nur noch die beiden Normalspannungen${{\sigma }_{x}},{{\sigma }_{y}}$ und die Schubspannung${{\tau }_{xy}}={{\tau }_{yx}}$aktiv. Sie sind jeweils über die gesamte Dicke der Scheibe konstant.
Wird die Scheibe nicht senkrecht bzw. parallel zu den jeweiligen Achsen, sondern unter einem Winkel $\varphi $ geschnitten, müssen die Spannungen (${{\sigma }_{x}},{{\sigma }_{y}}$und ${{\tau }_{xy}}$) unter Berücksichtigung des Schnittwinkels $\varphi $ mithilfe der Transformationsgleichungen (in ${{\sigma }_{\xi }},{{\sigma }_{\eta }}$ und${{\tau }_{\zeta \eta }}$) umgerechnet werden.
Bei einem bestimmten Schnittwinkel herrschen die maximalen Spannungen am Scheibenelement. Die diesem Schnitt angetragenen Normalspannungen heißen Hauptspannungen ${{\sigma }_{1}}$ und ${{\sigma }_{2}}$. Sie stehen senkrecht aufeinander und bilden das Hauptachsensystem. Die erste Hauptspannung ${{\sigma }_{1}}$ wird größer als die zweite Hauptspannung ${{\sigma }_{2}}$ angenommen.
State of plane stress
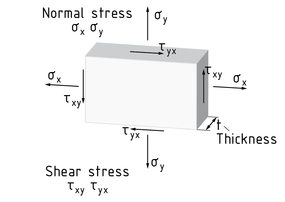
The state of plane stress prevails in slices of minimal thickness t . It can thus be assumed that stresses are acting in two dimensions. Only the two normal stresses${{\sigma }_{x}},{{\sigma }_{y}}$ and the shear stress${{\tau }_{xy}}={{\tau }_{yx}}$ are still active. In each case, they are constant over the entire thickness of the slice.
If the slice is not perpendicular or parallel to the relevant axes but at an angle $\varphi $, the stresses (${{\sigma }_{x}},{{\sigma }_{y}}$and ${{\tau }_{xy}}$) must be converted (into ${{\sigma }_{\xi }},{{\sigma }_{\eta }}$ and${{\tau }_{\zeta \eta }}$) using the transformation equations and taking into account the angle of intersection $\varphi $.
The maximum stresses act on the slice element at a particular angle of intersection. The normal stresses applied to this section are called principal stresses ${{\sigma }_{1}}$ and ${{\sigma }_{2}}$. They are mutually perpendicular and form the principal coordinate system. The first principal stress ${{\sigma }_{1}}$ is assumed to be greater than the second principal stress ${{\sigma }_{2}}$.
Estado de esfuerzo plano
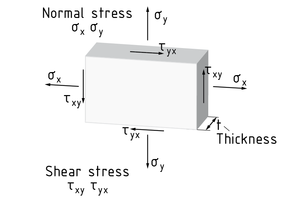
El estado de esfuerzo plano prevalece en rebanadas de espesor mínimo t . Puede, por lo tanto, asumirse que los esfuerzos actúan en dos dimensiones. Solo los dos esfuerzos normales ${{\sigma }_{x}},{{\sigma }_{y}}$ y el esfuerzo de corte ${{\tau }_{xy}}={{\tau }_{yx}}$ permanecen activos. En cada caso, son constantes sobre el espesor entero de la rebanada.
Estado de esfuerzo plano en una rebanada
Si la rebanada no es perpendicular ni paralela a los ejes relevantes, sino que es angular $\varphi $ , los esfuerzos (${{\sigma }_{x}},{{\sigma }_{y}}$y ${{\tau }_{xy}}$) deben ser convertidos (en ${{\sigma }_{\xi }},{{\sigma }_{\eta }}$ y${{\tau }_{\zeta \eta }}$) usando las ecuaciones de transformación y considerando el ángulo de intersección $\varphi $ .
Los esfuerzos máximos actúan en el elemento de rebanada en un ángulo en particular de la intersección. Los esfuerzos normales aplicados a esta sección se llaman esfuerzos principales ${{\sigma }_{1}}$ y ${{\sigma }_{2}}$ . Son mutuamente perpendiculares y forman el sistema de coordenadas principal. Se supone que el primer esfuerzo principal ${{\sigma }_{1}}$ es mayor que el segundo esfuerzo principal ${{\sigma }_{2}}$ .
