欧拉法

Geometrische Darstellung des Euler-Chauchy-Verfahrens

欧拉法 （折线法）是一种求解常微分方程（柯西）初值问题的简单数值方法。例如，欧拉法可以得到那些难以求解或不能精确求解的方程的近似解。欧拉法也被称为“小步骤法”，这是因为每一步通常都要求解一个非线性方程。

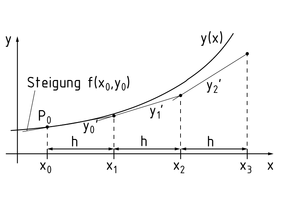
显式（或前进）欧拉法（欧拉-柯西法）是最简单的单步迭代法，它从给定的初值 ${{y}_{0}}=y({{x}_{0}})$ 开始，利用迭代公式 ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n}},{{y}_{n}})$ 进行计算。这里的 $h\cdot f({{x}_{n}},{{y}_{n}})$ 表示切线斜率。但是这种方法误差很大，而且多数情况下仅适用于步长 h 很小的情形，这是因为这里的导数仅仅是在单点处获得，进而推导得到其他值。

隐式（或后退）欧拉法是一种基于给定的初值 ${{y}_{0}}=y({{x}_{0}})$ 和迭代公式 ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n+1}},{{y}_{n+1}})$ 进行计算的单步法。这种方法之所以称为隐式法，是因为等式右边与 ${{y}_{n+1}}$ 有关，而且每一步都涉及到利用已知的 ${{x}_{n}}$, ${{y}_{n}}$ 和 ${{y}_{n+1}}$ 求解 ${{y}_{n+1}}$ 的迭代过程，例如，使用根试解的方法。这种方法可以得到更加稳定的结果。选择的步长 h越小，近似值的精确度就越高。

然而，欧拉法对于求解连续系统或进行较长期的预测时精确度却很差。龙格-库塔法使用更多的插值节点，以不同的方式提高了精度评估及其对预测值的影响。

欧拉-柯西法的几何解释

近义词

折线法

Euler-Verfahren

Geometrische Darstellung des Euler-Chauchy-Verfahrens

Mit dem Euler-Verfahren (Polygonzug-Verfahren) sind Anfangswertprobleme bei gewöhnlichen Differentialgleichungen auf eine einfache Art numerisch zu lösen. So können etwa Lösungen für schwer oder nicht explizit lösbare Differentialgleichungen näherungsweise gefunden werden. Das Euler-Verfahren wird auch als 'Verfahren der kleinen Schritte' bezeichnet, weil in jedem Schritt eine meist nichtlineare Gleichung zu lösen ist.

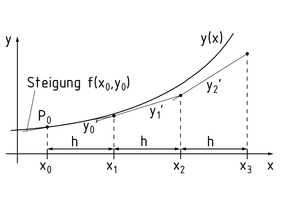
• Beim expliziten Euler-Verfahren (Euler-Cauchy) als einfachstem Einschrittverfahren steht mit ${{y}_{0}}=y({{x}_{0}})$ ein gegebener Anfangswert mit Iterationsvorschrift ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n}},{{y}_{n}})$. Dabei stellt $h\cdot f({{x}_{n}},{{y}_{n}})$ die Steigung dar. Das recht grobe Verfahren ist überwiegend für kleine h geeignet, weil die Ableitung nur an einem Punkt gewonnen und dann extrapoliert wird.
• Beim impliziten Euler-Verfahren als Einschrittverfahren steht mit ${{y}_{0}}=y({{x}_{0}})$ ein gegebener Anfangswert mit Iterationsvorschrift ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n+1}},{{y}_{n+1}})$. Es wird als implizit bezeichnet, weil die rechte Seite von ${{y}_{n+1}}$ abhängig ist und in jedem Schritt für bekannte ${{x}_{n}}$, ${{y}_{n}}$ und ${{y}_{n+1}}$ die Iterationsvorschrift für ${{y}_{n+1}}$ beispielsweise über eine Nullstellensuche zu lösen ist. Dafür liefert es stabilere Ergebnisse. Je kleiner die gewählte Schrittweite h ist, desto genauer sind die approximierten Werte.

Für kontinuierliche Systeme oder längere Prognosezeiträume sind die Euler-Verfahren jedoch zu ungenau. Das Runge-Kutta-Verfahren verwendet mehr Stützstellen und bewertet ihren Einfluss auf den Prognosewert unterschiedlich, so dass es zu einer höheren Genauigkeit führt.

Euler method

Geometrical illustration of the Euler-Chauchy method

The Euler method (polygonal method) is a simple numerical method for solving initial-value (Cauchy) problems with ordinary differential equations. For example, it enables solutions to be found by approximation for differential equations that are difficult to solve or cannot be solved explicitly. The Euler method is also called the 'method of small steps' because each step involves solving a mostly non-linear equation.

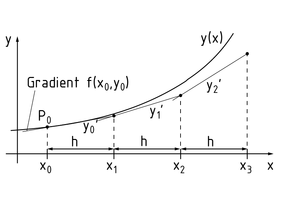
• The explicit (or forward) Euler method (Euler-Cauchy), the simplest single-step method, is based on a specified initial value ${{y}_{0}}=y({{x}_{0}})$ with an iteration process ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n}},{{y}_{n}})$. In this case, $h\cdot f({{x}_{n}},{{y}_{n}})$ represents the gradient. This very rough method is mainly suitable for small h values because the derivative is obtained at a single point only and then extrapolated.
• The implicit (or backward) Euler method is a single-step method based on a specific initial value ${{y}_{0}}=y({{x}_{0}})$ with an iteration process ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n+1}},{{y}_{n+1}})$. It is called implicit because the right-hand side is dependent on ${{y}_{n+1}}$ and each step involves solving the iteration process for ${{y}_{n+1}}$ for known values of ${{x}_{n}}$, ${{y}_{n}}$ and ${{y}_{n+1}}$, for example using a root search. This produces more stable results. The smaller the selected step size h, the more accurate the approximated values.

However, Euler methods are too imprecise for continuous systems or lengthy forecasting periods. The Runge-Kutta method uses more interpolation nodes and assesses their impact on the forecast value in different ways, which improves the accuracy.

Método de Euler

Ilustración geométrica del método de Euler-Cauchy

El método de Euler (método poligonal) es un método numérico simple para resolver problemas de valor inicial (Cauchy) con ecuaciones diferenciales ordinarias. Por ejemplo, permite encontrar soluciones mediante aproximación para ecuaciones diferenciales que son difíciles de resolver o no pueden resolverse de manera explícita. El método de Euler también se llama "método de los pasos pequeños", ya que cada paso involucra resolver una ecuación principalmente no lineal.

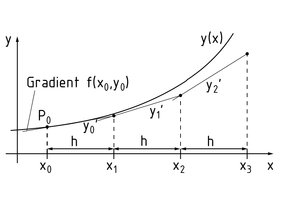
El método de Euler (Euler-Cauchy) explícito (o directo), el método de paso único más simple, se basa en el valor inicial especificado ${{y}_{0}}=y({{x}_{0}})$ con un proceso de iteración ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n}},{{y}_{n}})$ . En este caso, $h\cdot f({{x}_{n}},{{y}_{n}})$ representa el gradiente. Este método muy aproximado es adecuado principalmente para valores de h muy pequeños, ya que la derivada se obtiene en un punto único solamente y luego se extrapola.

El método de Euler (Euler-Cauchy) implícito (o al revés), es un método de paso único más simple basado en un valor inicial específico ${{y}_{0}}=y({{x}_{0}})$ con un proceso de iteración ${{y}_{n+1}}={{y}_{n}}+h\cdot f({{x}_{n+1}},{{y}_{n+1}})$ . Se llama implícito debido a que el lado derecho es independiente en ${{y}_{n+1}}$ y cada paso involucra resolver el proceso de iteración para ${{y}_{n+1}}$ para los valores conocidos de ${{x}_{n}}$ , ${{y}_{n}}$ y ${{y}_{n+1}}$ , por ejemplo, usando una búsqueda de raíz. Esto produce resultados más estables. Mientras más pequeño sea el tamaño de paso seleccionado h, más precisos serán los valores aproximados.

Sin embargo, los métodos de Euler son demasiado imprecisos para los sistemas continuos o para periodos de pronósticos largos. El método de Runge-Kutta usa más nodos de interpolación y evalúa su impacto en el valor de pronóstico de diferentes maneras, lo que mejora la precisión.

Ilustración geométrica del método de Euler-Cauchy